
����Ŀ��Ϊ��ʵ������̩�ݡ��Ĺ��������������ƻ��Գ�����·���и��죬�ְ��żס����������̶���ɸø��칤��.��֪�ӵĹ���Ч�����Ҷӹ���Ч�ʵ�![]() �����Ӹ���720�ĵ�·���ҶӸ���ͬ�����ĵ�·����4��.
�����Ӹ���720�ĵ�·���ҶӸ���ͬ�����ĵ�·����4��.
(1)�ס��������̶�ÿ���ܸ����·�ij��ȷֱ��Ƕ����ף�
(2)���ӹ���һ���踶����7��Ԫ���Ҷӹ���һ���踶����5��Ԫ���������ĵ�·ȫ��2400�ף������ܷ��ò�����195��Ԫ�������ٰ��żӹ��������죿
���𰸡�(1)�ס��������̶�ÿ���ܸ����·�ij��ȷֱ�90�ף�60�ף�(2)���ٰ��żӹ���10��.
��������
��1�����ݼӸ���720�ĵ�·���ҶӸ���ͬ�����ĵ�·����4�����г����̣��ⷽ�̼��ɣ���2�������ٰ��żӹ���m�죬���ݡ������ܷ��ò�����195��Ԫ���г�����ʽ���ⲻ��ʽ����
(1)����x����![]()
�ɵó�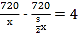
���x=60��������x=60��ԭ���̵Ľ�
��Ϊ90����Ϊ60
(2)�����ٰ��żӹ���m�죬��![]()
![]()
m��10
�����ٰ��ż�10��.


 ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��ڽ����ڼ俪չ�Żݴ����������ԭ�۳���500Ԫ����Ʒ������500Ԫ�IJ��ֿ������ܴ����Żݣ���������Ʒ��ʵ�ʸ�����y(��λ��Ԫ)����Ʒԭ��x(��λ��Ԫ)�ĺ�����ϵ��ͼ����ͼ��ʾ����500Ԫ�IJ��ֿ������ܵ��Ż���( )

A. ������B. ������C. �����D. �����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ������Բ����
������Բ����![]() �ڵ�һ�����ֵ�Բ���˶�������
�ڵ�һ�����ֵ�Բ���˶�������![]() ������
������![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ������˵������
������˵������![]() ����
����![]() ����
����![]() �����ֵΪ10.������ȷ���ǣ� ��
�����ֵΪ10.������ȷ���ǣ� ��
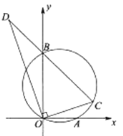
A. �٢�B. �ڢ�C. �٢�D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ϊ�˽Ȿ�еĿ�������������ӻ�������������ȡ��������Ŀ������������Ϊ��������ͳ�ƣ���������ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��������Ϣδ��������
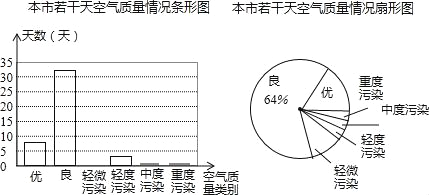
����������Ϣ�����½��۴�����ǣ� ��
A������ȡ������Ϊ50��
B����������Ⱦ����ռ����Ϊ10%
C������ͳ��ͼ�б�ʾ�ŵ����ε�Բ�ĽǶ���57.6��
D�����Ƹ�����һ��ﵽ�ź�����������������290��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ᆳ����Ϊij��������һ�ֽ������ϣ�����Ĵ�����ָ����������ṩ��Դ���������۳����ٽ��н��㣬δ�۳����ɳ��Ҹ�����������ÿ���ۼ�Ϊ260Ԫʱ����������Ϊ45�֣��þ�����Ϊ��߾�Ӫ��������ȡ���۵ķ�ʽ���д��������г����鷢�֣���ÿ���ۼ�ÿ�½�10Ԫʱ�����������ͻ�����7.5�֣��ۺϿ��Ǹ������أ�ÿ�۳�һ�ֽ������Ϲ���֧�����Ҽ���������100Ԫ��
��1����ÿ���ۼ���240Ԫʱ�������ʱ������������
��2������ѭ��������������ԭ���£���ÿ�ֲ����ۼ�Ϊ����ʱ���þ������������Ϊ9000Ԫ��
��3��С��˵���������������ʱ�������۶�Ҳ�������Ϊ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̽���봴�£�����֪A��B�������Ϸֱ��ʾa��b
����������������
a | 6 | ��6 | ��6 | 2 | ��1.5 |
b | 4 | 0 | ��4 | ��10 | ��1.5 |
A��B����ľ��� | 2 | �� �� | �� �� | �� �� | 0 |
����A��B�����ľ����Ϊd����d��a��b֮���к�������ϵ����ֱ��д�������
���������ϱ�����з���������������Pʹ����5�ͩ�5�ľ���֮��Ϊ10�������������Щ�����ĺͣ�
![]()
������Q��ʾ����Ϊx������Q��ʲôλ��ʱ��|x+1|+|x��2|����Сֵ����Сֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��ת������
��ת������![]() �غ�.
�غ�.
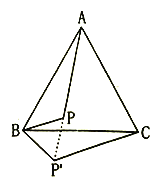
��1����ת��������һ�㣿
��2����ת�Ƕ��Ƕ��ٶȣ�
��3������![]() ��
��![]() ��ʲô�����Σ���˵������.
��ʲô�����Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
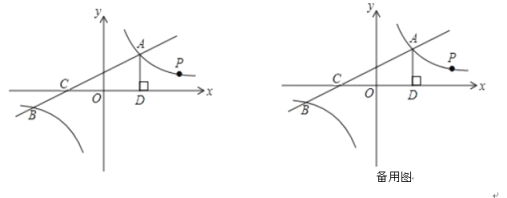
����Ŀ����ͼ��һ�κ���y1��k1x+2�뷴��������![]() ��ͼ���ڵ�A��4��m����B����8����2����x�ύ�ڵ�C������A��AD��x���ڵ�D
��ͼ���ڵ�A��4��m����B����8����2����x�ύ�ڵ�C������A��AD��x���ڵ�D
��1����һ�κ����뷴���������Ľ���ʽ��
��2�����ݺ���ͼ��֪����y1��y2ʱ��x��ȡֵ��Χ�� ��
��3������BD�����ABD�����
��4����P�Ƿ����������ڵ�һ����ͼ����һ�㣬��ֱ��OP���߶�AD���ڵ�E������ODE�ס�CDAʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
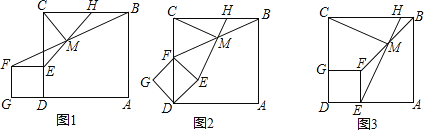
����Ŀ����ͼ1����E��������ABCD��CD������һ�㣬��DEΪ����������DEFG������BF����M���߶�BF�е㣬����EM��BC���ڵ�H������CM��
��1����ֱ��д��CM��EM��������ϵ��λ�ù�ϵ��
��2����ͼ1�е�������DEFG�Ƶ�D˳ʱ����ת45������ʱ��Fǡ�������߶�CD�ϣ���ͼ2�������������䣬��1���еĽ����Ƿ��������˵�����ɣ�
��3����ͼ1�е�������DEFG�Ƶ�D˳ʱ����ת90������ʱ��E��Gǡ�÷ֱ������߶�AD��CD�ϣ���ͼ3�������������䣬��1���еĽ����Ƿ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com