
【题目】如图,点O为原点,⊙O的半径为1,点A的坐标为(2,0),动点B在⊙O上,以AB为边作等边△ABC(顺时针),则线段OC的最小值为_____.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,平移一条抛物线,如果平移后的新抛物线经过原抛物线顶点,且新抛物线的对称轴是y轴,那么新抛物线称为原抛物线的“影子抛物线”.
中,平移一条抛物线,如果平移后的新抛物线经过原抛物线顶点,且新抛物线的对称轴是y轴,那么新抛物线称为原抛物线的“影子抛物线”.
(1)已知原抛物线表达式是![]() ,求它的“影子抛物线”的表达式;
,求它的“影子抛物线”的表达式;
(2)已知原抛物线经过点(1,0),且它的“影子抛物线”的表达式是![]() ,求原抛物线的表达式;
,求原抛物线的表达式;
(3)小明研究后提出:“如果两条不重合的抛物线交y轴于同一点,且它们有相同的“影子抛物线”,那么这两条抛物线的顶点一定关于y轴对称.”你认为这个结论成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙、丙三人组成的篮球训练小组,他们三人之间进行互相传球练习,篮球从一个人手中随机传到另外一个人手中计作传球一次,共连续传球三次.
(1)若开始时篮球在甲手中,则经过第一次传球后,篮球落在丙的手中的概率是 ;
(2)若开始时篮球在甲手中,求经过连续三次传球后,篮球传到乙的手中的概率.(请用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷3枚硬币做游戏,其中1元硬币1枚,5角硬币两枚.
(1)求3枚硬币同时正面朝上的概率.
(2)小张、小王约定:正面朝上按面值算,背面朝上按0元算.3枚落地后,若面值和为1.5元,则小张获得1分;若面值和为1元,则小王得1分.谁先得到10分,谁获胜,请问这个游戏是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,P是边AD上的一动点,连接BP、CP,过点B作射线交线段CP的延长线于点E,交AD边于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y.
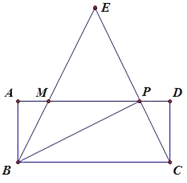
(1)说明△ABM∽△APB;并求出y关于x的函数关系式,写出自变量x的取值范围;
(2)当AP=4时,求sin∠EBP的值;
(3)如果△EBC是以∠EBC为底角的等腰三角形,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有任意三角形,当这个三角形的一条边上的中线等于这条边的一半时,称这个三角形叫“和谐三角形”,这条边叫“和谐边”,这条中线的长度叫“和谐距离”.
(1)已知A(2,0),B(0,4),C(1,2),D(4,1),这个点中,能与点O组成“和谐三角形”的点是 ,“和谐距离”是 ;
(2)连接BD,点M,N是BD上任意两个动点(点M,N不重合),点E是平面内任意一点,△EMN是以MN为“和谐边”的“和谐三角形”,求点E的横坐标t的取值范围;
(3)已知⊙O的半径为2,点P是⊙O上的一动点,点Q是平面内任意一点,△OPQ是“和谐三角形”,且“和谐距离”是2,请描述出点Q所在位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的弦,过
的弦,过![]() 的中点
的中点![]() 作
作![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,使得
,使得![]() .
.
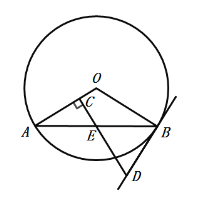
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的
的![]() 边上的高.
边上的高.
(3)在(2)的条件下,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com