
ЁОЬтФПЁП![]() дкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌжБЯпyЃНЉx+4гыxжсНЛгкЕуAЃЌЙ§ЕуAЕФХзЮяЯпyЃНax2+bxгыжБЯпyЃНЉx+4НЛгкСэвЛЕуBЃЌЧвЕуBЕФКсзјБъЮЊ1ЃЎ
дкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌжБЯпyЃНЉx+4гыxжсНЛгкЕуAЃЌЙ§ЕуAЕФХзЮяЯпyЃНax2+bxгыжБЯпyЃНЉx+4НЛгкСэвЛЕуBЃЌЧвЕуBЕФКсзјБъЮЊ1ЃЎ



ЃЈ1ЃЉИУХзЮяЯпЕФНтЮіЪНЮЊЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌQЮЊХзЮяЯпЩЯЮЛгкжБЯпABЩЯЗНЕФвЛЖЏЕуЃЈВЛгыBЁЂAжиКЯЃЉЃЌЙ§QзїQPЁЭxжсЃЌНЛxжсгкPЃЌСЌНгAQЃЌMЮЊAQжаЕуЃЌСЌНгPMЃЌЙ§MзїMNЁЭPMНЛжБЯпABгкNЃЌШєЕуPЕФКсзјБъЮЊtЃЌЕуNЕФКсзјБъЮЊnЃЌЧѓnгыtЕФКЏЪ§ЙиЯЕЪНЃЛдкДЫЬѕМўЯТЃЌШчЭМ2ЃЌСЌНгQNВЂбгГЄЃЌНЛyжсгкEЃЌСЌНгAEЃЌЧѓtЮЊКЮжЕЪБЃЌMNЁЮAEЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌНЋжБЯпABШЦЕуAЫГЪБеыа§зЊ15ЖШНЛХзЮяЯпЖдГЦжсгкЕуCЃЌЕуTЮЊЯпЖЮOAЩЯЕФвЛЖЏЕуЃЈВЛгыOЁЂAжиКЯЃЉЃЌвдЕуOЮЊдВаФЁЂвдOTЮЊАыОЖЕФдВЛЁгыЯпЖЮOCНЛгкЕуDЃЌвдЕуAЮЊдВаФЁЂвдATЮЊАыОЖЕФдВЛЁгыЯпЖЮACНЛгкЕуFЃЌСЌНгDFЃЎдкЕуTдЫЖЏЕФЙ§ГЬжаЃЌЫФБпаЮODFAЕФУцЛ§газюДѓжЕЛЙЪЧгазюаЁжЕЃПЧыЧѓГіИУжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+4xЃЛЃЈ2ЃЉnЃН![]() ЃЌЃЈ0ЃМtЃМ3ЃЉЃЛ tЃН2ЪБЃЌMNЁЮAEЃЛЃЈ3ЃЉдкЕуTдЫЖЏЕФЙ§ГЬжаЃЌЫФБпаЮODFAЕФУцЛ§газюаЁжЕЮЊ3
ЃЌЃЈ0ЃМtЃМ3ЃЉЃЛ tЃН2ЪБЃЌMNЁЮAEЃЛЃЈ3ЃЉдкЕуTдЫЖЏЕФЙ§ГЬжаЃЌЫФБпаЮODFAЕФУцЛ§газюаЁжЕЮЊ3![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЕуAЁЂBЕФзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЃЌМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙ§ЕуMзїMGЁЭxжсгкGЃЌNHЁЭGMгкHЃЎЯШжЄУїNЁЂPЁЂAШ§ЕудквдMЮЊдВаФMAЮЊАыОЖЕФЁбMЩЯЃЌШЛКѓЕУЕНЁїNMHЁеЁїMPGЃЌЕУЕНNHЃНMGЃЌHMЃНPGЃЌдйЩшPЮЊЃЈtЃЌ0ЃЉЃЌШЛКѓЙЙНЈЙигкtЕФЗНГЬЃЌНтЗНГЬМДПЩЕУЕНtЕФжЕЃЛ
ЃЈ3ЃЉЩшOT=mЃЌЫФБпаЮODFAЕФУцЛ§ЮЊSЃЌCDЃНAFЃНATЃН4ЉmЃЌCFЃНOTЃНmЃЌЙ§DзїDRЁЭACЃЌДЙзуЮЊRЃЌдђDRЃНDCsin60ЁуЃН![]() ЃЈ4ЉmЃЉЃЌдйгЩSЃНSЁїOACЉSЁїCDFМДПЩЕУГіНсТлЃЎ
ЃЈ4ЉmЃЉЃЌдйгЩSЃНSЁїOACЉSЁїCDFМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЁпжБЯпyЃНЉx+4гыxжсНЛгкЕуAЃЌ
Сюy=0ЃЌдђx=4ЃЌ
ЁрЕуAЮЊЃЈ4ЃЌ0ЃЉЃЌ
ЁпжБЯпyЃНЉx+4ОЙ§ЕуBЃЌЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрЕуBЕФзнзјБъЮЊЃКyЃНЉ1+4=3ЃЌ
ЁрЕуBЮЊЃКЃЈ1ЃЌ3ЃЉЃЌ
АбЕуAЁЂBДњШыyЃНax2+bxЃЌЕУ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуMзїMGЁЭxжсгкGЃЌNHЁЭGMгкHЃЎ
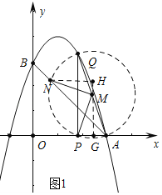
ЁпOAЃНOBЃЌЁЯAOBЃН90ЁуЃЌ
ЁрЁЯPANЃН45ЁуЃЌ
ЁпЁЯNMPЃН90ЁуЃЌ
ЁрЁЯPANЃН![]() ЁЯNMPЃЌ
ЁЯNMPЃЌ
ЁрNЁЂPЁЂAШ§ЕудквдMЮЊдВаФMAЮЊАыОЖЕФЁбMЩЯЃЌ
ЁрMNЃНMPЃЌ
ЁпЁЯNHMЃНЁЯPGMЃНЁЯNMPЃН90ЁуЃЌ
ЁрЁЯNMH+ЁЯPMGЃН90ЁуЃЌЁЯPMG+ЁЯMPGЃН90ЁуЃЌ
ЁрЁЯNMHЃНЁЯMPGЃЌ
ЁрЁїNMHЁеЁїMPGЃЌ
ЁрNHЃНMGЃЌHMЃНPGЃЌ
ЁпPЃЈtЃЌ0ЃЉЃЌ
ЁрQЃЈtЃЌЉt2+4tЃЉЃЌMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁрMGЃНNH
Ёр![]() ЉnЃН
ЉnЃН![]()
ЁрnЃН![]() ЃЌЃЈ0ЃМtЃМ3ЃЉЃЎ
ЃЌЃЈ0ЃМtЃМ3ЃЉЃЎ
ЁпMNЁЮAEЃЌQMЃНMAЃЌ
ЁрENЃНQNЃЌ
ЁрNЮЊEQжаЕуЃЌМДNx=![]()
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёрt2Љ4t+4ЃН0ЃЌ
НтЕУЃКtЃН2
ЁрtЃН2ЪБЃЌMNЁЮAEЃЎ
ЃЈ3ЃЉЫФБпаЮODFAЕФУцЛ§газюаЁжЕЃЎ
ЩшOTЃНmЃЌЫФБпаЮODFAЕФУцЛ§ЮЊS
ЁпCЪЧХзЮяЯпЖдГЦЩЯвЛЕуЃЌ
ЁрCOЃНCAЃЎ
ЁпжБЯпABШЦAЕуа§зЊ15ЁуЃЌ
ЁрЁЯOAC=60Ёу
ЁрЁїOACЪЧЕШБпШ§НЧаЮ
ЁпOAЃН4ЃЌSЁїOACЃН![]() ЁС42ЃН
ЁС42ЃН![]() ЃЌ
ЃЌ
ЁрCDЃНAFЃНATЃН4ЉmЃЌCFЃНOTЃНmЃЌ
Й§DзїDRЁЭACЃЌДЙзуЮЊRЃЌ
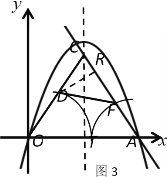
дђDRЃНDCsin60ЁуЃН![]() ЃЈ4ЉmЃЉЃЌ
ЃЈ4ЉmЃЉЃЌ
ЁрSЁїCDFЃН![]() CFDRЃН
CFDRЃН![]() m
m![]() ЃЈ4ЉmЃЉЃНЉ
ЃЈ4ЉmЃЉЃНЉ![]() m2+
m2+![]() mЃЌ
mЃЌ
ЁрSЃНSЁїOACЉSЁїCDF
ЃН4![]() ЉЃЈЉ
ЉЃЈЉ![]() m2+
m2+![]() mЃЉ
mЃЉ
ЃН![]() ЃЈmЉ2ЃЉ2+3
ЃЈmЉ2ЃЉ2+3![]() ЃЎ
ЃЎ
ЁрдкЕуTдЫЖЏЕФЙ§ГЬжаЃЌЫФБпаЮODFAЕФУцЛ§газюаЁжЕЮЊ3![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЕФжБОЖ
ЕФжБОЖ![]() ЃЌ
ЃЌ![]() ЮЊдВжмЩЯвЛЕуЃЌ
ЮЊдВжмЩЯвЛЕуЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЕФЧаЯп
ЕФЧаЯп![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЕФДЙЯп
ЕФДЙЯп![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЃЎ
ЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРюРЯЪІЮЊСЫСЫНтбЇЩњЪюЦкдкМвЕФдФЖСЧщПіЃЌЫцЛњЕїВщСЫ20УћбЇЩњФГвЛЬьЕФдФЖСаЁЪБЪ§ЃЌОпЬхЧщПіЭГМЦШчЯТЃК
дФЖСЪБМфЃЈаЁЪБЃЉ | 2 | 2.5 | 3 | 3.5 | 4 |
бЇЩњШЫЪ§ЃЈУћЃЉ | 1 | 2 | 8 | 6 | 3 |
дђЙигкет20УћбЇЩњдФЖСаЁЪБЪ§ЕФЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A. жкЪ§ЪЧ8 B. жаЮЛЪ§ЪЧ3
C. ЦНОљЪ§ЪЧ3 D. ЗНВюЪЧ0.34
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇЮЊСЫРЉДѓЩњВњЙцФЃЃЌМЦЛЎЙКТђ5ЬЈ![]() СНжжаЭКХЕФЩшБИЃЌзмзЪН№ВЛГЌЙ§28ЭђдЊЃЌЧввЊЧѓаТЙКТђЕФЩшБИЕФШезмВњСПВЛЕЭгк24ЭђМўЃЌСНжжаЭКХЩшБИЕФМлИёКЭШеВњСПШчЯТБэЃЎЮЊСЫНкдМзЪН№ЃЌЮЪгІбЁдёКЮжжЙКТђЗНАИЃП
СНжжаЭКХЕФЩшБИЃЌзмзЪН№ВЛГЌЙ§28ЭђдЊЃЌЧввЊЧѓаТЙКТђЕФЩшБИЕФШезмВњСПВЛЕЭгк24ЭђМўЃЌСНжжаЭКХЩшБИЕФМлИёКЭШеВњСПШчЯТБэЃЎЮЊСЫНкдМзЪН№ЃЌЮЪгІбЁдёКЮжжЙКТђЗНАИЃП
A | B | |
МлИёЃЈЭђдЊ/ЬЈЃЉ | 6 | 5 |
ШеВњСПЃЈЭђМў/ЬЈЃЉ | 6 | 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
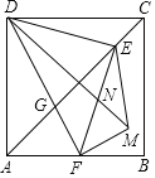
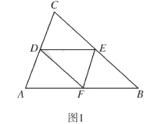
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌADЃН6ЃЌЕуEЪЧЖдНЧЯпACЩЯвЛЕуЃЌСЌНгDEЃЌЙ§ЕуEзїEFЁЭEDЃЌНЛABгкЕуFЃЌСЌНгDFЃЌНЛACгкЕуGЃЌНЋЁїEFGбиEFЗелЃЌЕУЕНЁїEFMЃЌСЌНгDMЃЌНЛEFгкЕуNЃЌШєAF=2ЃЌдђ![]() ЕФУцЛ§ЮЊ__ЃЎ
ЕФУцЛ§ЮЊ__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋЕШбќШ§НЧаЮ![]() елЕўЃЌЪЙЖЅЕу
елЕўЃЌЪЙЖЅЕу![]() гыЕзБп
гыЕзБп![]() ЕФжаЕу
ЕФжаЕу![]() жиКЯЃЌелЯпЗжБ№НЛ
жиКЯЃЌелЯпЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌбгГЄ![]() жСЕу
жСЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌВЂбгГЄ
ЃЌВЂбгГЄ![]() НЛ
НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМ2жаЕФЫљгаЦНааЫФБпаЮЃЈВЛАќРЈвд
ЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМ2жаЕФЫљгаЦНааЫФБпаЮЃЈВЛАќРЈвд![]() ЮЊвЛБпЕФЦНааЫФБпаЮЃЉ
ЮЊвЛБпЕФЦНааЫФБпаЮЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
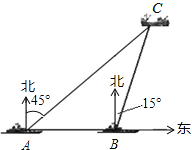
ЁОЬтФПЁПЕігуЕКздЙХвдРДОЭЪЧЮвЙњЕФЩёЪЅСьЭСЃЌЮЊЮЌЛЄЙњМвжїШЈКЭКЃбѓШЈРћЃЌЮвЙњКЃМрКЭгцеўВПУХЖдЕігуЕККЃгђЪЕЯжСЫГЃЬЌЛЏбВКНЙмРэЃЎШчЭМЃЌФГШедкЮвЙњЕігуЕКИННќКЃгђгаСНЫвздЮїЯђЖЋКНааЕФКЃМрДЌAЁЂBЃЌBДЌдкAДЌЕФе§ЖЋЗНЯђЃЌЧвСНДЌБЃГж20КЃРяЕФОрРыЃЌФГвЛЪБПЬСНКЃМрДЌЭЌЪБВтЕУдкAЕФЖЋББЗНЯђЃЌBЕФББЦЋЖЋ15ЁуЗНЯђгавЛЮвЙњгцеўжДЗЈДЌCЃЌЧѓДЫЪБДЌCгыДЌBЕФОрРыЪЧЖрЩйЃЎЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ25ЃЌФкВПга6ИіШЋЕШЕФе§ЗНаЮЃЌаЁе§ЗНаЮЕФЖЅЕуEЁЂFЁЂGЁЂHЗжБ№ТфдкБпADЁЂABЁЂBCЁЂCDЩЯЃЌдђУПИіаЁе§ЗНаЮЕФБпГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌвдЯТСаНсТле§ШЗЕФЪЧ(ЁЁЁЁ)
ЕФЭМЯѓШчЭМЫљЪОЃЌвдЯТСаНсТле§ШЗЕФЪЧ(ЁЁЁЁ)
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() (mЮЊШЮвтЪЕЪ§)ЃЎ
(mЮЊШЮвтЪЕЪ§)ЃЎ
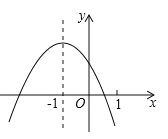
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com