
����Ŀ����ͼ����Rt��ABC�У�![]() ������һ�㹻���ֱ�����ǰ壬����ֱ�Ƕ���D��BC����һ�㣬������ֱ�DZ߷ֱ�AB��AC�ڵ�E��F.
������һ�㹻���ֱ�����ǰ壬����ֱ�Ƕ���D��BC����һ�㣬������ֱ�DZ߷ֱ�AB��AC�ڵ�E��F.

��1����ͼ1����DE��AB��DF��AC����֤���ı���AEDF�Ǿ���
��2���ڣ�1�������£�����D�ڡ�BAC�Ľ�ƽ�����ϣ����жϴ�ʱ�ı���AEDF��״����˵�����ɣ�
��3������D�ڡ�BAC�Ľ�ƽ�����ϣ���ֱ�����ǰ��Ƶ�D��תһ���ĽǶȣ�ʹ��ֱ�����ǰ��������������ֱ�DZ߷ֱ��ڵ�E��F����ͼ2������֤��![]() .�������������ߣ�
.�������������ߣ�
���𰸡���1�������� ��2�������Σ����ɼ����� ��3��������
��������
��1���ɴ�ֱ�Ķ���õ���AED=��AFD=90�������ݾ��ε��ж��������ɵõ����ۣ�
��2�����ݽ�ƽ���ߵ����ʵõ�DE=DF�����������ε��ж��������ɵõ�����AEDF�������Σ�
��3����DM��AB��M��DN��AC��N��֤���ı���AMDN�������Σ��������ε����ʵõ�AM=DM=DN=AN����MDN=��AMD=90��������ǵ����ʵõ���NDF=��EDM������ȫ�������ε����ʵõ�EM=FN�����ݹ��ɶ����õ�AD=![]() AM������AM=
AM������AM=![]() ��AM+AN��=
��AM+AN��=![]() ��AE+AF���������������ɵõ����ۣ�
��AE+AF���������������ɵõ����ۣ�
��1����DE��AB��BF��AC��
���AED=��AFD=90����
�ߡ�BAC=90����
���ı���AEDF�Ǿ��Σ�
��2���ı���AEDF�������Σ�
���ɣ��ߵ�D�ڡ�BAC�� ��ƽ�����ϣ�DE��AB��BF��AC��
��DE=DF��
�����AEDF��������
��3����DM��AB��M��DN��AC��N��
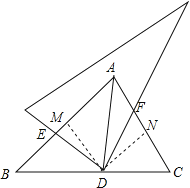
���AMD=��AND=��BAC=90����
�ߵ�D�ڡ�BAC�� ��ƽ�����ϣ�
��DM=DN��
���ı���AMDN�������Σ�
��AM=DM=DN=AN����MDN=��AMD=90����
���MDF+��NDF=90����
�ߡ�EDF=90����
���MDF+��EDM=90����
���NDF=��EDM��
����EMD����FND��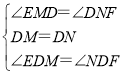 ��
��
���EMD�ա�FND��
��EM=FN��
�ߡ�AMD=90����
��AM2+DM2=AD2��
��AD=![]() AM��
AM��
��AM=![]() ��AM+AN��=
��AM+AN��=![]() ��AE+AF����
��AE+AF����
��AD=![]() ��
��![]() ��AE+AF����
��AE+AF����
��AE+AF=![]() AD��
AD��


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д� ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2�ǹ���x�ķ���x2��kx+5��k��5����0��������ʵ������������2x1+x2��7����ʵ��k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C=90�㣬�������߳���������������ż������AC��BC.
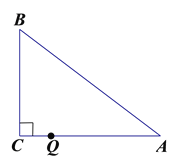
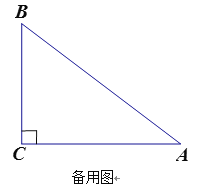
(1)���ֱ�������εĸ��߳���
(2)������Q�ӵ�C��������CA������1����λ����/����ٶ��˶��������Aֹͣ�˶��������ó߹���ͼ�����Ե�QΪԲ�ģ�QCΪ�뾶������AB�����е�Բ���������ʱ��Q���˶�ʱ��.
(3) ������Q�ӵ�C��������CA������1����λ����/����ٶ��˶�,�����Aֹͣ�˶�����QΪԲ�ġ�QC��Ϊ�뾶��Բ����̽����Q�������˶������У��˶�ʱ��tΪ������ֵʱ����Q���AB�ֱ���0�������㡢1���������2�������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
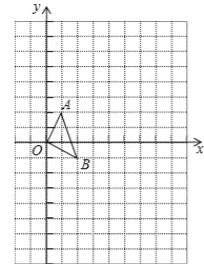
����Ŀ����ͼ���������������У�ÿһ��С�����εı߳���Ϊ1����OAB�Ķ���ֱ�ΪO��0��0����A��1��2����B��2����1����
��1���Ե�O��0��0��Ϊλ�����ģ���λ�Ʊ�1��3��λ�����ĵ�ͬ�ཫ��OAB�Ŵ�Ϊ��OA��B�䣬�Ŵ���A��B�Ķ�Ӧ��ֱ�ΪA�䡢B�䣬����ͼ�л�����OA��B�䣻
��2���ڣ�1���У���C��a��b��Ϊ�߶�AB����һ�㣬д���仯���C�Ķ�Ӧ��C'������____��
��3��ֱ��д���ı���ABA��B��������____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȥ�������в��ֵ��������˺����ĺ��֣���������������������ij��λ��ij����Сѧ����һ������ˮ���߲˹�320������������ˮ���߲˶�80����
��1��������ˮ���߲˸��ж��ټ���
��2���ּƻ����üס������ֻ�����8����һ���Խ���������ˮ���߲�ȫ������������Сѧ����֪ÿ�����ֻ�������װ����ˮ40�����߲�10����ÿ�����ֻ�������װ����ˮ���߲˸�20���������䲿�Ű��żס������ֻ���ʱ�м��ַ��������������Ƴ�����
��3���ڣ�2���������£�������ֻ���ÿ���踶�˷�400Ԫ�����ֻ���ÿ���踶�˷�360Ԫ�����䲿��Ӧѡ�����ַ�����ʹ�˷����٣������˷��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2��bx��c(a��0)��ͼ����ͼ��ʾ������ͼ�����������⣮
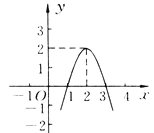
(1)�����ax2��bx��c��0����������
(2)д������ʽax2��bx��c��0�Ľ⼯��
(3)д��y��x���������С���Ա���x��ȡֵ��Χ��
(4)������ax2��bx��c��k����������ȵ�ʵ��������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ x �ķ��� 2x2+kx��1=0��
��1����֤����������������ȵ�ʵ������
��2�������̵�һ�����ǩ�1������һ������ k ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ��ٷ�չ��������ij�ҿ�ݹ�˾��2017��3�·���5�·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ10�����12.1������ּٶ��ù�˾ÿ��Ͷ�ݵĿ���ܼ�������������ͬ��
(1)��ÿ�ݹ�˾Ͷ�ݿ���ܼ�������ƽ����������
(2) ���ƽ��ÿ��ÿ������Ͷ�ݿ��0.6�������ô�ù�˾���е�21�����Ͷ��ҵ��Ա�ܷ����2017��6�·ݵĿ��Ͷ������������ܣ�����������Ҫ���Ӽ���ҵ��Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
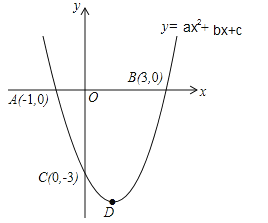
����Ŀ����ͼ��������![]() ��ͼ����x�ύ��A����1.0����B��3��0�����㣬��y�ύ�ڵ�C��0����3��������ΪD��
��ͼ����x�ύ��A����1.0����B��3��0�����㣬��y�ύ�ڵ�C��0����3��������ΪD��
��1����������ߵĽ���ʽ��
��2����������߶���D������ͶԳ��ᣮ
��3��̽���Գ������Ƿ����һ��P��ʹ���Ե�P��D��AΪ������������ǵ��������Σ������ڣ���������з���������P������꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com