
【题目】如图,平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,且
,且![]() ,点
,点![]() 为
为![]() 中点,
中点,![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
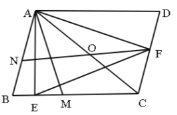
(1)若![]() ,求
,求![]() 的长度;
的长度;
(2)若![]() ,求证
,求证![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由等腰三角形三线合一得AE⊥BM,在Rt△ACE中,求出AE,再在Rt△AEM中求出AM即可;
(2)如图,作EH⊥AF于H,EG⊥DC交DC的延长线于G,由Rt△EHA≌Rt△EGC(HL),推出AH=CG,由Rt△EHF≌Rt△EGF(HL),推出FH=FG,由△AON≌△COF(ASA),推出AN=CF,推出AN+AF=FC+AF=FG-CG+FH+AH=2FH,由EF=![]() FH,即可解决问题
FH,即可解决问题
(1)解: ∵AB=AM,点![]() 为
为![]() 中点,
中点,
∴AE⊥BM,BE=EM=2
在Rt△ACE中,∵AC=![]() ,EC=EM+CM=5,
,EC=EM+CM=5,
∴AE=![]() =
=![]() ,
,
在Rt△AEM中,AM=![]() =
=![]() ;
;
(2)如图,作EH⊥AF于H,EG⊥DC交DC的延长线于G.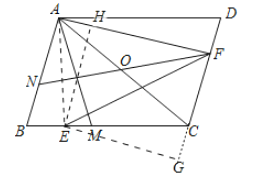
∵平行四边形![]() ,
,
∴AB∥CD,
∵![]()
∴AF⊥CD
∵AE⊥BM,
∵∠AEC=∠AFC=90°,
∵![]() ,
,
∴∠EFA=∠EFG=45°,∠EAC=45°,
∵EH⊥FA,EG⊥FG,
∴EH=EG,
∵∠ACE=∠EAC=45°,
∴AE=EC,
∴Rt△EHA≌Rt△EGC(HL),
∴AH=CG,
∵EF=EF,EH=EG,
∴Rt△EHF≌Rt△EGF(HL),
∴FH=FG,
∵AB∥CD,
∴∠OAN=∠OCF,
∵∠AON=∠COF,OA=OC,
∴△AON≌△COF(ASA),
∴AN=CF,
∴AN+AF=FC+AF=FG-CG+FH+AH=2FH,
∵∠EFA =45°,EH⊥FA,
∴EF=![]() FH,
FH,
∴AN+AF=![]() EF.
EF.


科目:初中数学 来源: 题型:
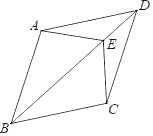
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果∠BDC=30°,DE=2,EC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣2,0),B(0,![]() ),C(4,0),其对称轴与x轴交于点D,若P为y轴上的一个动点,连接PD,
),C(4,0),其对称轴与x轴交于点D,若P为y轴上的一个动点,连接PD,![]() PB+PD的最小值为________.
PB+PD的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机销售商从厂家购进了![]() 两种型号的手机,已知一台
两种型号的手机,已知一台![]() 型手机的进价比一台
型手机的进价比一台![]() 型手机的进价多300元,用7500元购进
型手机的进价多300元,用7500元购进![]() 型手机和用6000元购进
型手机和用6000元购进![]() 型手机的数量相同.
型手机的数量相同.
(1)求一台![]() 型手机和一台
型手机和一台![]() 型手机的进价各是多少元?
型手机的进价各是多少元?
(2)在销售过程中,![]() 型手机因为性价比高,更受消费者的欢迎.为了增大
型手机因为性价比高,更受消费者的欢迎.为了增大![]() 型手机的销量,该销售商决定对
型手机的销量,该销售商决定对![]() 型手机进行降价销售.经调查,当
型手机进行降价销售.经调查,当![]() 型手机的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台.如果每天销售
型手机的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台.如果每天销售![]() 型手机的利润为3200元,请问该手机销售商应将
型手机的利润为3200元,请问该手机销售商应将![]() 型手机的售价降低多少元?
型手机的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
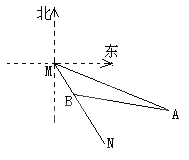
【题目】如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心.以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m.通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?(![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
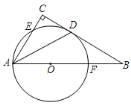
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E、F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
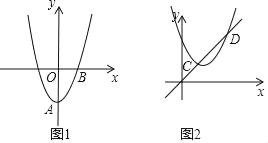
【题目】如图1,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣a2关于y轴对称且有最小值﹣1.
(1)求抛物线C1的解析式;
(2)在图1中抛物线C1顶点为A,将抛物线C1绕 点B旋转180°后得到抛物线C2,直线y=kx﹣2k+4总经过一定点M,若过定点M的直线与抛物线C2只有一个公共点,求直线l的解析式.
(3)如图2,先将抛物线 C1向上平移使其顶点在原点O,再将其顶点沿直线y=x平移得到抛物线C3,设抛物线C3与直线y=x交于C、D两点,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加学校秋季运动会,有以下 5 个项目可供选择:径赛项目:100m、200m、1000m(分别用 A1、A2、A3 表示);田赛项目:跳远,跳高(分别用 T1、T2 表示).
(1)该同学从 5 个项目中任选一个,恰好是田赛项目的概率 P 为 ;
(2)该同学从 5 个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率 P1,利用列表法或树状图加以说明;
(3)该同学从 5 个项目中任选两个,则两个项目都是径赛项目的概率 P2 为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com