
分析 先化简题目中的式子,然后令化简后的式子的值等于-1,求得x的值,再检验x的值是否使得原分式有意义,即可解答本题.
解答 解:$({\frac{2x}{x-1}-\frac{{{x^2}-x}}{{{x^2}-2x+1}}})÷\frac{x}{x+1}$
=$[\frac{2x}{x-1}-\frac{x(x-1)}{(x-1)^{2}}]÷\frac{x}{x+1}$
=$(\frac{2x}{x-1}-\frac{x}{x-1})×\frac{x+1}{x}$
=$\frac{x}{x-1}×\frac{x+1}{x}$
=$\frac{x+1}{x-1}$,
当$\frac{x+1}{x-1}=-1$时,解得,x=0,
当x=0时,原分式无意义,
故原代数式的值不能等于-1.
点评 本题考查分式的混合运算,解答本题的关键是明确分式的混合运算的计算方法,注意求得的x的值必须使得原分式有意义.


科目:初中数学 来源: 题型:选择题
| A. | 4.65×109 | B. | 4.65×1010 | C. | 4.65×1011 | D. | 4.65×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
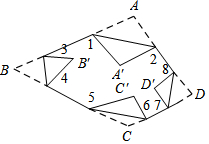 如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.
如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com