
【题目】已知抛物线 ![]()

(1)此抛物线的顶点坐标是 ,与x轴的交点坐标是 , ,与y轴交点坐标是 ,对称轴直线是 ;
(2)在平面直角坐标系中画出 ![]() 的图象;
的图象;
(3)结合图象,说明当x取何值时,y随x的增大而减小.
【答案】
(1)(1,-4);(3,0);(-1,0);(0,-3);x=1
(2)
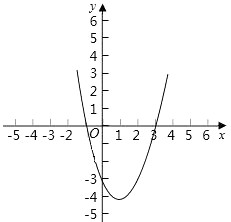
(3)
解:由图象可知当 x < 1时,y 随 x 的增大而减小.
【解析】(1)∵ ![]() ,∴抛物线顶点坐标为(1,-4),对称轴为直线x=1;
,∴抛物线顶点坐标为(1,-4),对称轴为直线x=1;
令y=0,可得 ![]() ,解得x=3或-1,∴抛物线与x轴的交点坐标为(3,0)和(-1,0);
,解得x=3或-1,∴抛物线与x轴的交点坐标为(3,0)和(-1,0);
令x=0可得y=-3,∴抛物线与y轴的交点坐标为(0,-3),
故答案依次为(1,-4),(3,0),(-1,0),(0,-3),x=1.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位) 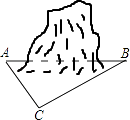
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点A、C在双曲线y1= ![]() 上,B、D在双曲线y2=
上,B、D在双曲线y2= ![]() 上,k1=2k2(k1>0),AB//y轴,S□ABCD=24,则k1=.
上,k1=2k2(k1>0),AB//y轴,S□ABCD=24,则k1=.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+1经过点(2,6),且与直线 ![]() 相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( ) 
A.![]() ﹣
﹣ ![]()
B.![]() ﹣2
﹣2 ![]()
C.π﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( ) 
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com