
【题目】一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( ) 
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
【答案】A
【解析】解:∵四边形ABCD是矩形, ∴AB=CD=3cm,AD=BC=5cm,
∵将纸片沿ED折叠,A点刚好落在BC边上的A'处,
∴A′D=AD=5cm,A′E=AE,
在Rt△A′CD中,根据勾股定理得,A′C= ![]() =
= ![]() =4cm,
=4cm,
所以,A′B=BC﹣A′C=5﹣4=1cm,
设AE=x,则BE=AB﹣AE=3﹣x,
在Rt△A′EB中,根据勾股定理得,A′B2+BE2=A′E2 ,
即12+(3﹣x)2=x2 ,
解得x= ![]() ,
,
即AE= ![]() cm.
cm.
故选A.
【考点精析】本题主要考查了翻折变换(折叠问题)的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知抛物线 ![]()

(1)此抛物线的顶点坐标是 ,与x轴的交点坐标是 , ,与y轴交点坐标是 ,对称轴直线是 ;
(2)在平面直角坐标系中画出 ![]() 的图象;
的图象;
(3)结合图象,说明当x取何值时,y随x的增大而减小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )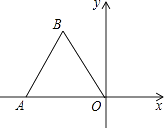
A.(1, ![]() )
)
B.(﹣1,2)
C.(﹣1, ![]() )
)
D.(﹣1, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3经过A(﹣1,0)B(4,0)两点,与y轴交于点C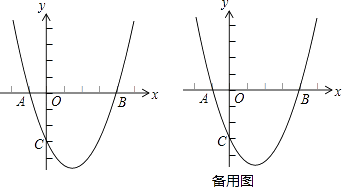
(1)求抛物线解析式;
(2)点N是x轴下方抛物线上的一点,连接AN,若tan∠BAN=2,求点N的纵坐标;
(3)点D是点C关于抛物线对称轴的对称点,连接AD,在x轴上是否存在E,使∠AED=∠CAD?如果存在,请直接写出点E坐标,如果不存在,请说明理由;
(4)连接AC、BC,△ABC的中线BM交y轴于点H,过点A作AG⊥BC,垂足为G,点F是线段BH上的一个动点(不与B、H重合),点F沿线段BH从点B向H移动,移动后的点记作点F′,连接F′C、F′A,△F′AC的F′C、F′A两边上的高交于点P,连接AP,CP,△F′AC与△PAC的面积分别记为S1 , S2 , S1和S2的乘积记为m,在点F的移动过程中,探究m的值变化情况,若变化,请直接写出m的变化范围,若不变,直接写出这个m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图(1),PAB为⊙O的割线,直线PC与⊙O有公共点C,且PC2=PA×PB,
(1)求证:∠PCA=∠PBC;直线PC是⊙O的切线;
(2)如图(2),作弦CD,使CD⊥AB,连接AD、BC,若AD=2,BC=6,求⊙O的半径;
(3)如图(3),若⊙O的半径为 ![]() ,PO=
,PO= ![]() ,MO=2,∠POM=90°,⊙O上是否存在一点Q,使得PQ+
,MO=2,∠POM=90°,⊙O上是否存在一点Q,使得PQ+ ![]() QM有最小值?若存在,请求出这个最小值;若不存在,说明理由.
QM有最小值?若存在,请求出这个最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为 . 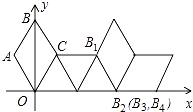
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,
在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,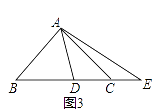
若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( ) 
A.2010年至2014年间工业生产总值逐年增加
B.2014年的工业生产总值比前一年增加了40亿元
C.2012年与2013年每一年与前一年比,其增长额相同
D.从2011年至2014年,每一年与前一年比,2014年的增长率最大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com