
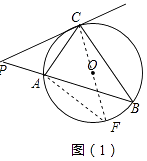
【题目】已知,如图(1),PAB为⊙O的割线,直线PC与⊙O有公共点C,且PC2=PA×PB,
(1)求证:∠PCA=∠PBC;直线PC是⊙O的切线;
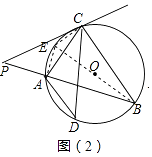
(2)如图(2),作弦CD,使CD⊥AB,连接AD、BC,若AD=2,BC=6,求⊙O的半径;
(3)如图(3),若⊙O的半径为 ![]() ,PO=
,PO= ![]() ,MO=2,∠POM=90°,⊙O上是否存在一点Q,使得PQ+
,MO=2,∠POM=90°,⊙O上是否存在一点Q,使得PQ+ ![]() QM有最小值?若存在,请求出这个最小值;若不存在,说明理由.
QM有最小值?若存在,请求出这个最小值;若不存在,说明理由.
【答案】
(1)
证明:∵PC2=PA×PB,
∴ ![]() ,
,
∵∠CPA=∠BPC,
∴△PCA∽△PBC,
∴∠PCA=∠PBC,
作直径CF,连接AF,则∠CAF=90°,
∴∠F+∠FCA=90°,
∵∠F=∠B,∠PCA=∠PBC,
∴∠PCA+∠FCA=90°,
∵PC经过直径的一端点C,
∴直线PC是⊙O的切线
(2)
解:作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,
∵CD⊥AB,
∴AE∥CD,
∴ ![]() =
= ![]() ,
,
∴AD=CE=2,
∵BC=6,
∴在Rt△BCE中,由勾股定理得:
BE2=CE2+BC2=22+62=40,
∴BE=2 ![]() ,
,
∴R= ![]()
(3)
解:取OM中点G,连接PG与⊙O的交点就是符合条件的点Q,
连接QO、QM,
∵MO=2,
∴OG= ![]() OM=1,
OM=1,
∵⊙O的半径r=OQ= ![]() ,
,
∴OQ2=OGOM,
∵∠MOQ=∠QOG,
∴△MOQ∽△QOG,
∴ ![]() =
= ![]() ,
,
∴QG= ![]() QM,
QM,
∴PQ+ ![]() QM=PQ+QG=PG,
QM=PQ+QG=PG,
根据两点之间线段最短,
此时PQ+ ![]() QM=PQ+QG=PG最小,
QM=PQ+QG=PG最小,
∴PQ+ ![]() QM最小值为PG=
QM最小值为PG= ![]() =
= ![]() =
= ![]() .
.

【解析】(1)根据已知条件得到 ![]() ,推出△PCA∽△PBC,根据相似三角形的性质得到∠PCA=∠PBC,作直径CF,连接AF,则∠CAF=90°,得到∠PCA+∠FCA=90°,P过直径的一端点C,于是得到结论;(2)作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,推出AE∥CD,得到
,推出△PCA∽△PBC,根据相似三角形的性质得到∠PCA=∠PBC,作直径CF,连接AF,则∠CAF=90°,得到∠PCA+∠FCA=90°,P过直径的一端点C,于是得到结论;(2)作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,推出AE∥CD,得到 ![]() =
= ![]() ,根据勾股定理得到BE=2
,根据勾股定理得到BE=2 ![]() ,于是得到结论;(3)取OM中点G,连接PG与⊙O的交点就是符合条件的点Q,连接QO、QM,得到OG=
,于是得到结论;(3)取OM中点G,连接PG与⊙O的交点就是符合条件的点Q,连接QO、QM,得到OG= ![]() OM=1,根据相似三角形的性质得到
OM=1,根据相似三角形的性质得到 ![]() =
= ![]() ,求得QG=
,求得QG= ![]() QM,根据两点之间线段最短,即可得到结论.
QM,根据两点之间线段最短,即可得到结论.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+1经过点(2,6),且与直线 ![]() 相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限.
(1)若AC所在直线的函数表达式是y=2x+4.
①求AC的长;
②求点B的坐标;
(2)若(1)中AC的长保持不变,点A在y轴的正半轴滑动,点C随之在x轴的负半轴上滑动.在滑动过程中,点B与原点O的最大距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( ) 
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y= ![]() x与双曲线y=
x与双曲线y= ![]() 相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC.若△PBC的面积是20,则点C的坐标为 .
相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC.若△PBC的面积是20,则点C的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= ![]() 在第一象限内的图象交于点P,且△POA的面积为2.
在第一象限内的图象交于点P,且△POA的面积为2. 
(1)求k的值.
(2)求平移后的直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)b= , c= , 点B的坐标为;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B两城市相距100km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)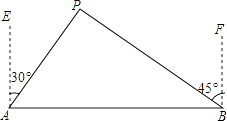
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com