
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= ![]() 在第一象限内的图象交于点P,且△POA的面积为2.
在第一象限内的图象交于点P,且△POA的面积为2. 
(1)求k的值.
(2)求平移后的直线的函数解析式.
【答案】
(1)解:∵点A(m,2)在直线y=2x,
∴2=2m,
∴m=1,
∴点A(1,2),
∵点A(1,2)在反比例函数y= ![]() 上,
上,
∴k=2
(2)解:方法一、如图,
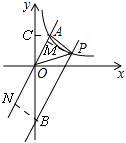
设平移后的直线与y轴相交于B,过点P作PM⊥OA,BN⊥OA,AC⊥y轴
由(1)知,A(1,2),
∴OA= ![]() ,sin∠BON=sin∠AOC=
,sin∠BON=sin∠AOC= ![]() =
= ![]() ,
,
∵S△POA= ![]() OA×PM=
OA×PM= ![]() ×
× ![]() PM=2,
PM=2,
∴PM= ![]() ,
,
∵PM⊥OA,BN⊥OA,
∴PM∥BN,
∵PB∥OA,
∴四边形BPMN是平行四边形,
∴BN=PM= ![]() ,
,
∵sin∠BON= ![]() =
= ![]() =
= ![]() ,
,
∴OB=4,
∵PB∥AO,
∴B(0,﹣4),
∴平移后的直线PB的函数解析式y=2x﹣4,
方法二、如图1,过点P作PC⊥y轴交OA于C,
设点P的坐标为(n, ![]() )(n>1),
)(n>1),
∴C( ![]() ,
, ![]() ),∴PC=n﹣
),∴PC=n﹣ ![]() ,
,
∵△POA的面积为2.A(1,2)
∴S△POA=S△PCO+S△PCA
= ![]() (n﹣
(n﹣ ![]() )×
)× ![]() +
+ ![]() (n﹣
(n﹣ ![]() )(2﹣
)(2﹣ ![]() )
)
= ![]() (n﹣
(n﹣ ![]() )×2
)×2
=n﹣ ![]()
=2,
∴n=1﹣ ![]() (舍)或n=1+
(舍)或n=1+ ![]() ,
,
∴P(1+ ![]() ,2
,2 ![]() ﹣2)
﹣2)
∴PB∥AO,
∴设直线PB的解析式为y=2x+b,
∵点P在直线PB上,
∴2 ![]() ﹣2=2(1+
﹣2=2(1+ ![]() )+b,
)+b,
∴b=﹣4,
∴平移后的直线PB的函数解析式y=2x﹣4,
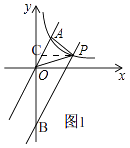
【解析】(1)由点A的纵坐标求得m,即点A的坐标,把点A的坐标代入反比例函数中即可;(2)方法一、先求出PM,再求出BN然后用锐角三角函数求出OB,即可.方法二、先设出点P的坐标,利用△POA的面积为2.建立方程求出点P的坐标,即可得出结论.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E. 
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图(1),PAB为⊙O的割线,直线PC与⊙O有公共点C,且PC2=PA×PB,
(1)求证:∠PCA=∠PBC;直线PC是⊙O的切线;
(2)如图(2),作弦CD,使CD⊥AB,连接AD、BC,若AD=2,BC=6,求⊙O的半径;
(3)如图(3),若⊙O的半径为 ![]() ,PO=
,PO= ![]() ,MO=2,∠POM=90°,⊙O上是否存在一点Q,使得PQ+
,MO=2,∠POM=90°,⊙O上是否存在一点Q,使得PQ+ ![]() QM有最小值?若存在,请求出这个最小值;若不存在,说明理由.
QM有最小值?若存在,请求出这个最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为 . 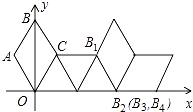
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,
在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,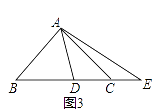
若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c与y轴交于点C,其顶点记为M,自变量x=﹣1和x=5对应的函数值相等.若点M在直线l:y=﹣12x+16上,点(3,﹣4)在抛物线上.
(1)求该抛物线的解析式;
(2)设y=ax2+bx+c对称轴右侧x轴上方的图象上任一点为P,在x轴上有一点A(﹣ ![]() ,0),试比较锐角∠PCO与∠ACO的大小(不必证明),并写出相应的P点横坐标x的取值范围.
,0),试比较锐角∠PCO与∠ACO的大小(不必证明),并写出相应的P点横坐标x的取值范围.
(3)直线l与抛物线另一交点记为B,Q为线段BM上一动点(点Q不与M重合),设Q点坐标为(t,n),过Q作QH⊥x轴于点H,将以点Q,H,O,C为顶点的四边形的面积S表示为t的函数,标出自变量t的取值范围,并求出S可能取得的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com