
【题目】如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为 . 
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= ![]() 在第一象限内的图象交于点P,且△POA的面积为2.
在第一象限内的图象交于点P,且△POA的面积为2. 
(1)求k的值.
(2)求平移后的直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)b= , c= , 点B的坐标为;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,某学校计划举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生必须从“A(洪家关),B(天门山),C(大峡谷),D(黄龙洞)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图. 
请你根据图中所提供的信息,完成下列问题:
(1)本次调查的学生人数为;
(2)在扇形统计图中,“天门山”部分所占圆心角的度数为;
(3)请将两个统计图补充完整;
(4)若该校共有2000名学生,估计该校最想去大峡谷的学生人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图. 
请根据图中信息,解答下列问题:
(1)参加初赛的选手共有名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A0(2,0)作直线l:y= ![]() x的垂线,垂足为点A1 , 过点A1作A1A2⊥x轴,垂足为点A2 , 过点A2作A2A3⊥l,垂足为点A3 , …,这样依次下去,得到一组线段:A0A1 , A1A2 , A2A3 , …,则线段A2016A2107的长为( )
x的垂线,垂足为点A1 , 过点A1作A1A2⊥x轴,垂足为点A2 , 过点A2作A2A3⊥l,垂足为点A3 , …,这样依次下去,得到一组线段:A0A1 , A1A2 , A2A3 , …,则线段A2016A2107的长为( )
A.( ![]() )2015
)2015
B.( ![]() )2016
)2016
C.( ![]() )2017
)2017
D.( ![]() )2018
)2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B两城市相距100km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)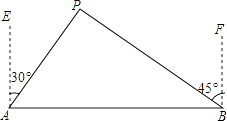
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=﹣ ![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD. 
(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD , 求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com