
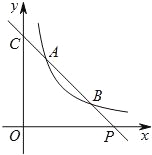
【题目】如图,已知直线y=ax+b与双曲线![]() (x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
【答案】(1)P点坐标为(4,0);
(2)A(2,2),B(4,1);
(3)x1+x2=x0.
【解析】
试题分析:(1)把A点坐标代入反比例函数解析式可求得k,进一步可求得B点坐标,再利用待定系数法可求得直线解析式,可求得P点坐标;
(2)过点A作AD∥x轴,交x轴于点D,利用△ACD∽△PCO,结合A、P、C的坐标可求得x1、y1之间的关系,结合AB=BP可表示出B点坐标,再结合A、B两点都在反比例函数图象上,可求得A、B两点的坐标;
(3)结合(1)、(2)中的坐标可猜得结论.
试题解析:(1)∵点A(1,3)在反比例函数y=![]() 上,∴k=3,
上,∴k=3,
∵点B(3,y2)在y=![]() 上,
上,
∴y2=1,即B点坐标为(3,1),
把A、B两点坐标代入直线y=ax+b,
可得![]() ,解得
,解得![]() ,∴直线AB的解析式为y=﹣x+4,
,∴直线AB的解析式为y=﹣x+4,
当y=0时,x=4,∴P点坐标为(4,0);
(2)如图,过A作AD∥x轴,交y轴于点D,则AD⊥y轴,
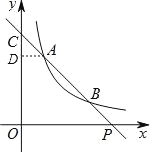
∴△ACD∽△PCO,∴![]() =
=![]() ,
,
∵b=y1+1,P(6,0),A(x1,y1),
∴CD=1,OC=y1+1,AD=x1,OP=6,
∴![]() =
=![]() ,
,
∵AB=BP,A(x1,y1),
∴B为AP中点,且P为(6,0),∴B点坐标为(![]() ,
,![]() ),∵A、B两点都在y=
),∵A、B两点都在y=![]() 上,∴x1y1=
上,∴x1y1=![]()
![]() ,解得x1=2,∴
,解得x1=2,∴![]() =
=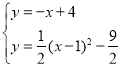 ,解得y1=2,∴A(2,2),B(4,1);
,解得y1=2,∴A(2,2),B(4,1);
(3)猜想x1,x2,x0之间的关系式为:x1+x2=x0.
理由如下:∵A(x1,y1),B(x2,y2),
∴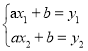 ,解得
,解得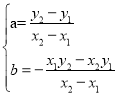 ,
,
∴直线AB解析式为y=![]() x﹣
x﹣![]() ,
,
令y=0可得x=![]() ,
,
∵x1y1=x2y2,
∴x=![]() =
=![]() =x1+x2,
=x1+x2,
即x1+x2=x0.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x(元) | 15 | 20 | 30 | … |
y(件) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)是销售价x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日的销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面网格中每个小正方形的边长为1. 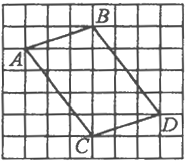
(1)线段CD是线段AB经过怎样的平移后得到的?
(2)线段AC是线段BD经过怎样的平移后得到的?
查看答案和解析>>
科目:初中数学 来源: 题型:
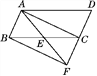
【题目】如图,已知点E是ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.
(1)连接AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形;
(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我国粮食生产首次实现了建国以来的“十连增”,全年粮食产量突破12000亿斤.将1 200 000 000 000用科学记数法表示为( )
A. 12×1011 B. 1.2×1011 C. 1.2×1012 D. 0.12×1013
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com