
【题目】如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则 ![]() 的值为( )
的值为( )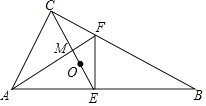
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵点O是△ABC的重心,
∴OC= ![]() CE,
CE,
∵△ABC是直角三角形,
∴CE=BE=AE,
∵∠B=30°,
∴∠FAE=∠B=30°,∠BAC=60°,
∴∠FAE=∠CAF=30°,△ACE是等边三角形,
∴CM= ![]() CE,
CE,
∴OM= ![]() CE﹣
CE﹣ ![]() CE=
CE= ![]() CE,即OM=
CE,即OM= ![]() AE,
AE,
∵BE=AE,
∴EF= ![]() AE,
AE,
∵EF⊥AB,
∴∠AFE=60°,
∴∠FEM=30°,
∴MF= ![]() EF,
EF,
∴MF= ![]() AE,
AE,
∴ ![]() =
= ![]() =
= ![]() .
.
故选:D.
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方).


科目:初中数学 来源: 题型:
【题目】如图,已知△ABD和△CEF都是斜边为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B、D、C、E都在同一直线上,DC=4.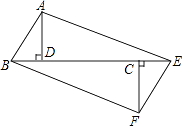
(1)求证:四边形ABFE是平行四边形.
(2)△ABD沿着BE的方向以每秒1cm的速度运动,设△ABD运动的时间为t秒,
①当t为何值时,ABFE是菱形?请说明你的理由.
②ABFE有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴、y轴上,反比例函数y= ![]() (x>0)的图像经过点D,且与边BC交于点E,则点E的坐标为.
(x>0)的图像经过点D,且与边BC交于点E,则点E的坐标为. 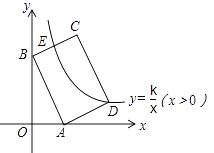
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD、CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于BP+EP最小值的是( )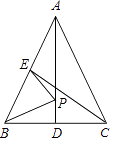
A.BC
B.CE
C.AD
D.AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元. 设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) | 0.5 | 2 | … | ||
乙复印店收费(元) | 0.6 | 2.4 | … |
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1 , y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“阅读季”活动,小明调查了班级里40名同学计划购书的花费情况,并将结果绘制成如图所示的条形统计图,根据图中相关信息,这次调查获取的样本数据的众数和中位数分别是( ) 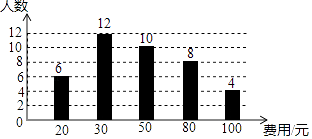
A.12和10
B.30和50
C.10和12
D.50和30.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com