
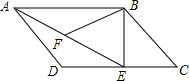
 如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.分析 (1)由平行的性质结合条件可得到∠AFB=∠EDA和∠BAE=∠AED,可证得结论;
(2)由平行可知∠ABE=90°,在Rt△ABE中,由直角三角形的性质结合勾股定理可求得AE,然后根据相似三角形的性质即可得到结论.
解答 (1)证明:∵AD∥BC,
∴∠C+∠ADE=180°,
∵∠BFE=∠C,
∴∠AFB=∠EDA,
∵AB∥DC,
∴∠BAE=∠AED,
∴△ABF∽△EAD;
(2)解:∵AB∥CD,BE⊥CD,
∴∠ABE=90°,
∵AB=4,∠BAE=30°,
∴AE=2BE,
由勾股定理可求得AE=$\frac{8\sqrt{3}}{3}$,
∵△ABF∽△EAD,
∴$\frac{BF}{AD}=\frac{AB}{AE}$,
即$\frac{BF}{3}=\frac{4}{\frac{8\sqrt{3}}{3}}$,
∴BF=$\frac{3\sqrt{3}}{2}$.
点评 本题主要考查相似三角形的判定和平行线的性质,掌握相似三角形的判定方法是解题的关键,即①有两组角对应相等、②两组边对应成比例且夹角相等、③三组边对应成比例的两个三角形相似.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
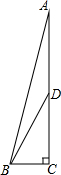 (1)计算:sin30°+3tan60°-cos245°.
(1)计算:sin30°+3tan60°-cos245°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
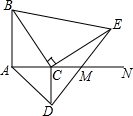 如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为4.
如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 火车在笔直的轨道上匀速行驶 | B. | 商场电梯上上下下运动 | ||
| C. | 滑雪运动员在平坦的雪地上滑行 | D. | 汽车玻璃上雨刷器的运动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com