
当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A ﹣2 B 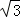 或
或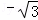 C 2或
C 2或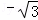 D 2或﹣
D 2或﹣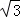 或
或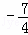
 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
在开展“国学诵读”活动中,某校为了解全校1 300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据.估计该校1 300名学生一周的课外阅读时间不少于7小时的人数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
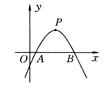
如图2 - 79所示,已知二次函数y=ax2+bx+c(a≠0)的图象的顶点p的横坐标是4,图象与x轴交于点A(m ,0)和点B,且点A在点B的左侧,那么线段AB的长是 .(用含字母m的代数式表示)
,0)和点B,且点A在点B的左侧,那么线段AB的长是 .(用含字母m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
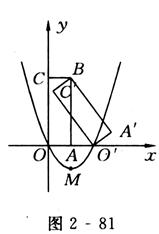
如图2 - 81所示,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕点B逆时针旋转得到的.点O′在x轴的正半轴上,点B的坐标为(1,3).
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O,O′两点,且图象顶点M的纵坐标为-l,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对 称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
(3)求边C′O′所在直线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com