
如图2 - 81所示,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕点B逆时针旋转得到的.点O′在x轴的正半轴上,点B的坐标为(1,3).
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O,O′两点,且图象顶点M的纵坐标为-l,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对 称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
(3)求边C′O′所在直线的解析式.
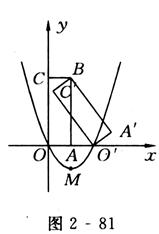
 解:(1)如图2-83所示,连接BO,BO′,则BO=BO′.∵BA⊥OO′,∴AO=AO′.∵B(1,3),∴O′(2,0),M(1,-1),∴
解:(1)如图2-83所示,连接BO,BO′,则BO=BO′.∵BA⊥OO′,∴AO=AO′.∵B(1,3),∴O′(2,0),M(1,-1),∴ 解得
解得 ∴所求二次函数的解析式为y=x2-2x.
∴所求二次函数的解析式为y=x2-2x.
(2)假设存在满足题设条件的点P(x,y).连接OM,PM,OP,过P作PN⊥x轴于N,则∠POM=90°.∵M(1,-1),A(1,0),AM=OA,∴∠NOA=45°,∴∠PON=45°,∴ON=NP,即x=y.∵P(x,y)在二次函数y=x2-2x的图象上,∴x=x2-2x,解得 x=0或x=3.∵P(x,y)在对称轴的右侧,∴x>1,∴x=3,y=3,即P(3,3)是所求的点.连接MO′,显然△OMO′为等腰直角三角形,∴点O′(2,0)也是满足条件的点,∴满足条件的点是P(2,0)或P(3,3),∴O
x=0或x=3.∵P(x,y)在对称轴的右侧,∴x>1,∴x=3,y=3,即P(3,3)是所求的点.连接MO′,显然△OMO′为等腰直角三角形,∴点O′(2,0)也是满足条件的点,∴满足条件的点是P(2,0)或P(3,3),∴O P=3
P=3 ,OM=
,OM= ,∴S△POM=
,∴S△POM= OP·OM=3或S△POM=
OP·OM=3或S△POM= OM·O′M=1.
OM·O′M=1.
(3)设AB与C′O′的交点为D(1,y),显然Rt△DAO′≌Rt△DC′B.在Rt△DAO′中,AO′2+AD2=O′D2,即1+y2=(3-y)2,解得y= ,∴D(1,
,∴D(1, ).设边C′O′所在直线的解析式为y=kx+b,则
).设边C′O′所在直线的解析式为y=kx+b,则 解得
解得 ∴所求直线的解析式为y=
∴所求直线的解析式为y=


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
已知一组数据x1,x2,…,xn的方差是s2,则新的一组数据ax1+1,ax2+1,…,axn+1(a为常数,a≠0)的方差是 .(用含有a,s2的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线y=x2-4x+3的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为( )
A.(4,-1 ) B.(0,-3) C.(-2,-3) D.(-2,-1)
) B.(0,-3) C.(-2,-3) D.(-2,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
用配方法把二次函数y=l+2x-x2化为y=a(x-h)2+k的形式,作出它的草图,回答下列问题.
(1)求抛物线的顶点坐标和它与x轴的交点坐标;
(2)当x取何值时,y随x的增大而增大?
(3)当x取何值时,y的值 大于0?
大于0?
查看答案和解析>>
科目:初中数学 来源: 题型:
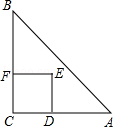
如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
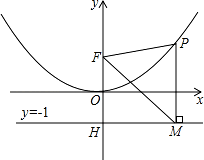
二次函数图象的顶点在原点O,经过点A(1,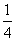 );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图2-114所示,在边长为8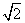 cm的正方形ABCD中,E,F是对角线AC上的两个点,它们分别从点A、点C同时出发,沿对角线以1 cm/s的相同速度运动,过E作EH垂直AC,交Rt△ADC的直角边于H;过F作FG垂直AC,交Rt△ADC的直角边于G,连接HG,EB. 设HE,EF,FG,GH围成的图形面积为S1,AE,EB,BA围成的图形面积为S2(这里
cm的正方形ABCD中,E,F是对角线AC上的两个点,它们分别从点A、点C同时出发,沿对角线以1 cm/s的相同速度运动,过E作EH垂直AC,交Rt△ADC的直角边于H;过F作FG垂直AC,交Rt△ADC的直角边于G,连接HG,EB. 设HE,EF,FG,GH围成的图形面积为S1,AE,EB,BA围成的图形面积为S2(这里 规定:线段的面积为0).若E到达C,F到达A
规定:线段的面积为0).若E到达C,F到达A ,则停止运动.若E的运动时间为x s,解答下列问题.
,则停止运动.若E的运动时间为x s,解答下列问题.
(1)当0<x<8时,直接写出以E,F,G,H为顶点的四边形是什么四边形,并求x为何值时,S1=S2;

(2)①若y是S1与S2的和,求y与x之间的函数关系式;(图2-115为备用图)②求y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
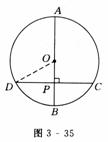
如图3-35所示,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6 cm,则直径AB的长是 ( )
A.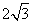 cm B.
cm B. cm
cm
C.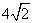 cm D.
cm D.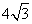 cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com