
【题目】如图,![]() ,
,![]() ,
,![]() .动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l(其解析式为
.动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l(其解析式为![]() ,且直线l与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.
,且直线l与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.

(1)当![]() 时,求l的解析式;
时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)求出t为何值时,点M关于l的对称点落在坐标轴上.
【答案】(1) ![]() ;(2) 6<t<9;(3) 2秒或3秒.
;(2) 6<t<9;(3) 2秒或3秒.
【解析】
(1)将P(0,4)代入解析式中即可求解;
(2)当直线l刚好经过M点时求出其与y轴的交点坐标,进而求出P点运动的路程,再除以速度进而得到时间;当直线l刚好经过N点时同样的方式求出时间,两个时间之间即为t的取值范围;
(3)作M点关于l的对称点M’,求出M’坐标,再分别令其横坐标和纵坐标为0,求出t的值.
解:(1)当![]() 时,此时P点的坐标为(0,5),将(0,5)代入解析式
时,此时P点的坐标为(0,5),将(0,5)代入解析式![]() 中
中
得到:![]() ,解得:
,解得:![]()
故![]() 时,求l的解析式为:
时,求l的解析式为:![]() .
.
故答案为:![]() .
.
(2)当直线l经过点![]() 时,将点
时,将点![]() 代入解析式
代入解析式![]() 中
中
得到:![]() ,解得:
,解得:![]() ,此时l的解析式为:
,此时l的解析式为:![]()
令![]() ,∴此时P点的坐标为
,∴此时P点的坐标为![]()
又∵运动的速度为1个单位每秒,故此时运动了7-1=6秒;
当直线l经过点![]() 时,将点
时,将点![]() 代入解析式
代入解析式![]() 中
中
得到:![]() ,解得:
,解得:![]() ,此时l的解析式为:
,此时l的解析式为:![]()
令![]() ,∴此时P点的坐标为
,∴此时P点的坐标为![]()
又∵运动的速度为1个单位每秒,故此时运动了10-1=9秒;
故当6<t<9时点M,N位于l的异侧.
故答案为:6<t<9.
(3) 作M点关于l的对称点M’,如下图所示:
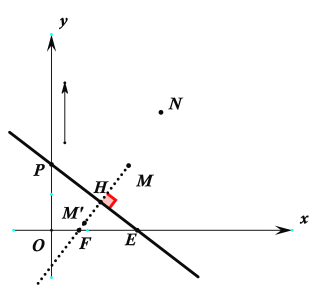
连接MM’与x轴交于点F,直线l与x轴交于E点,直线l与MM’交于点H
则有MM’⊥HE,∴∠EHF=90°
∵直线l与x轴所夹的锐角为45°
∴∠MFE=90°-45°=45°
∴直线MM’解析式中的k=1,设MM’解析式为y=x+n,
代入点M(4,3),解得n=-1
故直线MM’的解析式为:y=x-1
∴设点M’的坐标为(![]() ),
),
由H是M和M’的中点可知:
H点坐标为![]() ,即H
,即H![]()
情况一:当M’位于x轴上时,即![]() ,即
,即![]() 时,
时,
求得H点坐标为(![]()
又H点在直线l上,故将H点坐标代入直线l的解析式![]() 中
中
求得![]() ,此时l的解析式
,此时l的解析式![]()
∴此时P点坐标为(0,4)
故时间t=(4-1)÷1=3秒;
情况二:当M’位于y轴上时,即![]() 时
时
求得H点坐标为(![]()
又H点在直线l上,故将H点坐标代入直线l的解析式![]() 中
中
求得![]() ,此时l的解析式
,此时l的解析式![]()
∴此时P点坐标为(0,3)
故时间t=(3-1)÷1=2秒;
故答案为:2秒或3秒.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
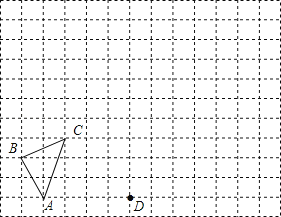
【题目】如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
(1)若点A、C的坐标分别为(﹣3,0)、(﹣2,3),请画出平面直角坐标系并指出点B的坐标;
(2)画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1;
(3)以图中的点D为位似中心,将△A1B1C1作位似变换且把边长放大到原来的两倍,得到△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是2019年5月17日至31日某市的空气质量指数趋势图.
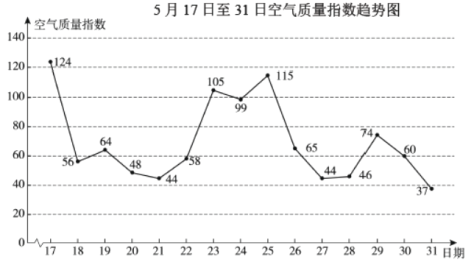
(说明:空气质量指数为0-50、51-100、101-150分别表示空气质量为优、良、轻度污染)
有如下结论:
①在此次统计中,空气质量为优的天数少于轻度污染的天数;
②在此次统计中,空气质量为优良的天数占![]() ;
;
③20,21,22三日的空气质量指数的方差小于26,27,28三日的空气质量指数的方差.
上述结论中,所有正确结论的序号是( )
A.①B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南浔区某校组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有120千米,队伍乘大巴车8:00从学校出发.苏老师因有事情,8:30从学校自驾小汽车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果比队伍提前10分钟到达基地.问:
(1)设大巴午的平均速度是x(km/h),利用速度、时间和路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)(温馨提示:请填写在答题卷相对应的表格内)
速度(km/h) | 路程(km) | 时间(h) | |
大巴车 | x | 120 | ________ |
小汽车 | ________ | 120 | ________ |
(2)列出方程,并求出大巴车与小汽车的平均速度.
(3)当苏老师追上大巴车时,大巴车离基地还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
档次 | 工资(元) | 频数(人) | 频率 |
A | 3000 | 20 | |
B | 2800 | 0.30 | |
C | 2200 | ||
D | 2000 | 10 |
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,部分同学随家长一同到某公园游玩,下面是购买门票时,甲同学与其爸爸的对话(如图),试根据图中的信息,解决下列问题:
票 价
成人:每人80元
学生:按成人票价五折优惠
团体票:16人以上(含16人),每人按成人票价六折优惠
 成人门票每张80元,学生门票五折优惠,我们一共12人,共需800元.
成人门票每张80元,学生门票五折优惠,我们一共12人,共需800元.
 爸爸,等一下,让我算一算,换一种方式,购票是否可以省钱.
爸爸,等一下,让我算一算,换一种方式,购票是否可以省钱.
(1)本次共去了几个成人,几个学生?
(2)甲同学所说的另一种购票方式,是否可以省钱?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )

A.(S.S.S.) B.(S.A.S.) C.(A.S.A.) D.(A.A.S.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
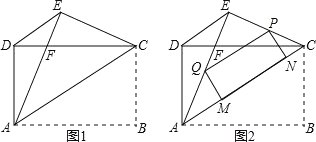
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y= ![]() 2+b
2+b![]() +c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)若M是抛物线的对称轴与直线BC的交点,N是抛物线的顶点,求MN的长;
(3)设点P是(1)中的抛物线的一个动点,是否存在满足S△PAB=8的点P?如存在请求出P的坐标;若不存在,请说明理由.


图1 备用图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com