
【题目】南浔区某校组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有120千米,队伍乘大巴车8:00从学校出发.苏老师因有事情,8:30从学校自驾小汽车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果比队伍提前10分钟到达基地.问:
(1)设大巴午的平均速度是x(km/h),利用速度、时间和路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)(温馨提示:请填写在答题卷相对应的表格内)
速度(km/h) | 路程(km) | 时间(h) | |
大巴车 | x | 120 | ________ |
小汽车 | ________ | 120 | ________ |
(2)列出方程,并求出大巴车与小汽车的平均速度.
(3)当苏老师追上大巴车时,大巴车离基地还有多远?
【答案】(1)1.5x;![]() ;
;![]() (2)60公里/小时,90公里/小时 (3)30公里
(2)60公里/小时,90公里/小时 (3)30公里
【解析】
(1)根据小汽车的速度=大巴车的速度×1.5,用含x的代数式表示出小汽车的速度;再利用时间=路程÷速度,分别用含x的代数式表示出两车的时间;
(2)抓住关键语句:队伍乘大巴车8:00从学校出发;苏老师8:30从学校自驾小汽车出发,结果比队伍提前10分钟到达基地.;此题的等量关系为:大巴车行驶120千米的路程所用的时间=小汽车行驶120千米的时间+![]() ,设未知数列方程,再解方程检验,即可求解;
,设未知数列方程,再解方程检验,即可求解;
(3)抓住已知条件:苏老师自驾小汽车追上大巴车后继续前行,结果比队伍提前10分钟到达基地.,据此设未知数,列方程求解即可.
解:(1)
速度(km/h) | 路程(km) | 时间(h) | |
大巴车 | x | 120 |
|
小汽车 | 1.5x | 120 |
|
(2)解:设大巴的平均速度为x公里/小时,则小车的平均速度为1.5x公里/小时,
根据题意,得: ![]()
解得:x=60,
经检验:x=60是原方程的解,
答:大巴的平均速度为60公里/小时,则小车的平均速度为90公里/小时;
(3)解:设苏老师赶上大巴的地点到基地的路程有y公里,
根据题意,得: ![]()
解得:y=30,
答:苏老师追上大巴车的地点到基地的路程有30公里.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
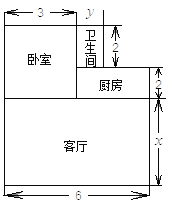
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)用含![]() 、
、![]() 的代数式表示地面总面积;
的代数式表示地面总面积;
(2)已知客厅面积比卫生间面积多21平方米,且地面总面积是卫生间面积的15倍.若铺1平方米地砖的平均费用为100元,那么铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
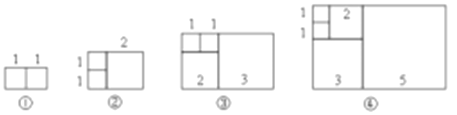
【题目】如图,将边长分别为1、2、3、5、…的若干正方形按一定的规律拼成不同的长方形,依次记作长方形①、长方形②、长方形③、长方形④,那么按此规律,长方形⑥的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,下列结论中正确的有( )
①当AB=BC时,它是菱形; ②当AC⊥BD时,它是菱形;
③当∠ABC=90°时,它是矩形; ④当AC=BD时,它是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
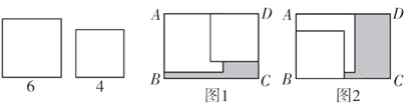
【题目】如图,已知在矩形ABCD内,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中末被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我围古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)“的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() .动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l(其解析式为
.动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l(其解析式为![]() ,且直线l与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.
,且直线l与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.

(1)当![]() 时,求l的解析式;
时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)求出t为何值时,点M关于l的对称点落在坐标轴上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
(1)请用直尺和圆规在图中直接作出∠A的平分线AE交BD于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,求出∠AED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
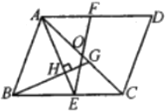
【题目】如图,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 是
是![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,解答下列问题:
,解答下列问题:
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com