
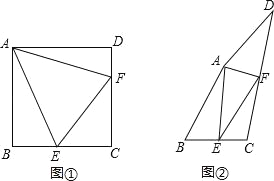
【题目】探究:如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连结EF,求证:EF=BE+DF.
应用:如图②,在四边形ABCD中,点E、F分别在BC、CD上,AB=AD,∠B+∠D=90°,∠EAF=![]() ∠BAD,若EF=3,BE=2,则DF= .
∠BAD,若EF=3,BE=2,则DF= .
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)如图①中,把△ABE绕点A逆时针旋转90°得到△ADE′,只要证明△AFE≌△AFE′即可解决问题.
(2)如图②中,将△ABE绕点A旋转到△ADE′位置连接E′F.,只要证明△FAE≌△FAE′得EF=FE′,在RT△E′DF中利用勾股定理即可解决问题.
试题解析:(1)如图①中,
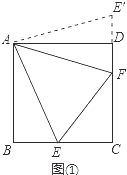
在正方形ABCD中,∵AB=AD,∠BAD=∠ADC=∠B=90°,
把△ABE绕点A逆时针旋转90°得到△ADE′,
∵∠ADF=∠ADE′=90°,
∴点F、D、E′共线,
∴∠E′AF=90°-45°=45°=∠EAF,
在△AFE和△AFE′中,
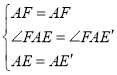 ,
,
∴△AFE≌△AFE′,
∵EF=FE′=DE′+DF=DE+DF.
(2)如图②中,
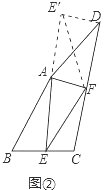
因为AB=AD,所以可以将△ABE绕点A旋转到△ADE′位置,连接E′F.
∵∠B+∠ADF=90°,∠B=∠E′DA,
∴∠E′DF=∠E′DA+′ADF=90°,
∵∠BAE+∠DAF=∠EAF,∠E′AD=∠BAE,
∴∠E′AF=∠EAF,
在△FAE和△FAE′中,
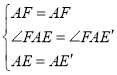 ,
,
∴△FAE≌△FAE′,
∴EF=FE′=3,
在RT△E′DF中,∵∠E′DF=90°,E′F=3,DE′=BE=2,
∴DF=![]() .
.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】下列运算中,结果正确的是( )
A. (a2b)2=a2b2B. (-m)7÷(-m)3=m4
C. (3xy2)2=6x2y4D. a6÷a2=a3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个正数的平方根和立方根都只有一个;
B. 0 的平方根和立方根都是0;
C. 1 的平方根与立方根都等于它本身;
D. 一个数的立方根与其自身相等的数只有-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四舍五入法按要求对0.06018分别取近似值,其中错误的是( )
A. 0.1(精确到0.1)
B. 0.06(精确到百分位)
C. 0.06(精确到千分位)
D. 0.0602(精确到0.0001)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
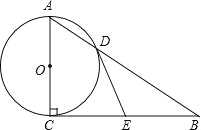
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com