
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1). 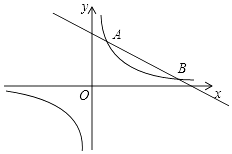
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
【答案】
(1)解:把点A(2,6)代入y= ![]() ,得m=12,
,得m=12,
则y= ![]() .
.
把点B(n,1)代入y= ![]() ,得n=12,
,得n=12,
则点B的坐标为(12,1).
由直线y=kx+b过点A(2,6),点B(12,1)得
![]() ,
,
解得 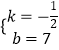 ,
,
则所求一次函数的表达式为y=﹣ ![]() x+7
x+7
(2)解:如图,直线AB与y轴的交点为P,设点E的坐标为(0,m),连接AE,BE,

则点P的坐标为(0,7).
∴PE=|m﹣7|.
∵S△AEB=S△BEP﹣S△AEP=10,
∴ ![]() ×|m﹣7|×(12﹣2)=10.
×|m﹣7|×(12﹣2)=10.
∴|m﹣7|=2.
∴m1=5,m2=9.
∴点E的坐标为(0,5)或(0,9).
【解析】(1)把点A的坐标代入反比例函数解析式,求出反比例函数的解析式,把点B的坐标代入已求出的反比例函数解析式,得出n的值,得出点B的坐标,再把A、B的坐标代入直线y=kx+b,求出k、b的值,从而得出一次函数的解析式;(2)设点E的坐标为(0,m),连接AE,BE,先求出点P的坐标(0,7),得出PE=|m﹣7|,根据S△AEB=S△BEP﹣S△AEP=10,求出m的值,从而得出点E的坐标.


科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为⊙O的直径,AB=4.动点P从A点出发,以每秒π个单位的速度在⊙O上按顺时针方向运动一周.设动点P的运动时间为t秒,点C是圆周上一点,且∠AOC=40°,当t=秒时,点P与点C中心对称,且对称中心在直径AB上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面一段:
计算![]()
观察发现,上式从第二项起,每项都是它前面一项的![]() 倍,如果将上式各项都乘以
倍,如果将上式各项都乘以![]() ,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.
,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.
解:设![]() ,①
,①
则![]() ,②
,②
②-①得![]() ,则
,则![]() .
.
上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例中是都等于![]() ),那么这列数的求和问题,均可用上述“错位相减”法来解决.
),那么这列数的求和问题,均可用上述“错位相减”法来解决.
下面请你观察算式![]() 是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果.
是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2(k-3)x+k2-4k-1=0.
(1)若这个方程有实数根,求k的取值范围;
(2)若这个方程有一个根为1,求k的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 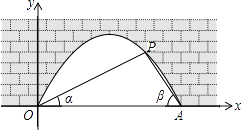
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b互为相反数,c,d互为倒数,m的绝对值是1,n是有理数且既不是正数也不是负数,求20161﹣(a+b)+m![]() ﹣(cd)2016+n(a+b+c+d)的值.
﹣(cd)2016+n(a+b+c+d)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1). 
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为a的正方形ABCD中,E、F是边AD,AB上两点(与端点不重合),且AE=BF.连接CE,DF相交于点M,
(1)当E为边AD的中点时,则DF的长为 (用含a的式子表示)
(2)求证:∠MCB+∠MFB=180°.
(3)点M能成为DF的中点吗?如果能,求出此时CM的长(用含a的式子表示);如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘坐一辆汽车沿东西方向的公路检修输电线路,规定向东为正,他们从A地出发到收工时,走过的路程记录如下:(单位:千米)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)他们收工时距A地多远?
(2)他们离出发点A最远时有多远?
(3)汽车每千米耗油![]() 升,从出发到返回A地共耗油多少升?
升,从出发到返回A地共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com