
【题目】如图,边长为a的正方形ABCD中,E、F是边AD,AB上两点(与端点不重合),且AE=BF.连接CE,DF相交于点M,
(1)当E为边AD的中点时,则DF的长为 (用含a的式子表示)
(2)求证:∠MCB+∠MFB=180°.
(3)点M能成为DF的中点吗?如果能,求出此时CM的长(用含a的式子表示);如果不能,说明理由.

【答案】(1)![]() (2)见解析(3)不能
(2)见解析(3)不能
【解析】分析:(1)当E为边AD的中点时,则F也是AB的中点,在Rt△ADF中,利用勾股定理求出DF的长;
(2)首先利用全等三角形的判定方法利用SAS证明△ADF≌△DCE,得到∠ADF=∠DCE,进而得出∠DME=90°,于是得到结论;
(3)假设点M成为DF的中点,利用垂直平分线的性质得到DC=CF,进而得到结论与题意不符.
详解:(1)∵E为边AD的中点,
∴F也为边AB边的中点,
∴AF=![]() AB=
AB=![]() a,
a,
在Rt△ADF中,
AD2+AF2=DF2,
∴DF=![]() ;
;
(2)∵在正方形ABCD中,
∴AB=BC=CD=AD,
又∵AE=BF,
∴AF=DE,
∵∠CDE=∠A=90°,
∴△ADF≌△DCE,
∴∠ADF=∠DCE,
∵∠DCE+∠DEC=90°,
∴∠ADF+∠DEC=90°,
∴∠DME=90°,
∴∠MCB+∠MFB=180°;
(3)假设点M成为DF的中点,
∵∠DME=90°,
∴DF⊥CE,
∵M成为DF的中点,
∴CM是DF的垂直平分线,
∴DC=CF,
∵DC=BC≠CF,
∴点M不能成为DF的中点.


科目:初中数学 来源: 题型:
【题目】如图是一份汽车票价表,李丽星期一、三、五要乘汽车上下班,星期二、四乘汽车上班,而搭朋友的车回家;她应该买什么样的票合算?如果周末她要乘汽车去公园,那么她选哪种票合算?
汽车公司票价表
单程票 |
|
周票 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1). 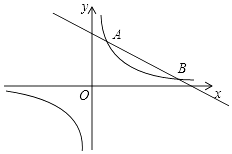
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(﹣6,8),C(﹣6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生数学科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:
完成作业 | 单元检测 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 |
(1)若按三项成绩的平均分记为期末评价成绩,请计算小张的期末评价成绩;
(2)若按完成作业、单元检测、期末考试三项成绩按1:2:m的权重,小张的期末评价成绩为81分,则小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com