
分析 根据第四象限内点的坐标特征得到不等式组,然后解不等式组即可.
解答 解:∵点P(3n+2,4-2n)在第四象限,
∴$\left\{\begin{array}{l}{3n+2>0}\\{4-2n<0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{n>-\frac{2}{3}}\\{n>2}\end{array}\right.$.
∴实数n的取值范围为:n>2.
点评 本题考查了点的坐标:我们把有顺序的两个数a和b组成的数对,叫做有序数对,记作(a,b).建立了坐标系的平面叫做坐标平面,两轴把此平面分成四部分,分别叫第一象限,第二象限,第三象限,第四象限.坐标轴上的点不属于任何一个象限;坐标平面内的点与有序实数对是一一对应的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为(5,-5).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为(5,-5).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
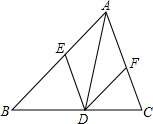 如图,已知AD是△ABC的角平分线,点E、F分别是边AC、AB的中点,连接DE、DF,要使四边形AEDF称为菱形,还需添加一个条件,这个条件可以是AB=AC、∠B=∠C或AE=AF(答案不唯一)..
如图,已知AD是△ABC的角平分线,点E、F分别是边AC、AB的中点,连接DE、DF,要使四边形AEDF称为菱形,还需添加一个条件,这个条件可以是AB=AC、∠B=∠C或AE=AF(答案不唯一)..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
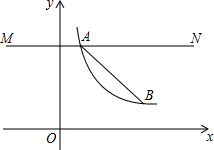 如图,点A、B是反比例函数第一象限图象上的两点,且坐标分别为(1,n),(n,$\frac{n}{4}$),直线MN过点A且与x轴平行.
如图,点A、B是反比例函数第一象限图象上的两点,且坐标分别为(1,n),(n,$\frac{n}{4}$),直线MN过点A且与x轴平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
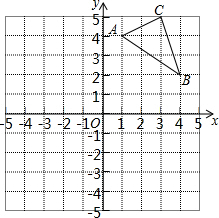 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
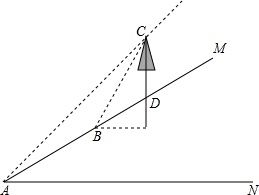 张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732)
张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com