
【题目】2018年我国科技实力进一步增强,嫦娥探月、北斗组网、航母海试、鲲龙击水、港珠澳大桥正式通车……,这些成就的取得离不开国家对科技研发的大力投入.下图是2014年—2018年我国研究与试验发展(R&D)经费支出及其增长速度情况. 2018年我国研究与试验发展(R&D)经费支出为19657亿元,比上年增长11.6%,其中基础研究经费1118亿元.
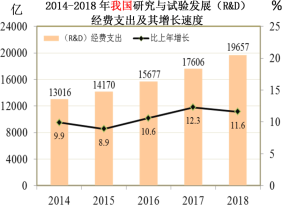
根据统计图提供的信息,下列说法中合理的是( )
A. 2014年—2018年,我国研究与试验发展(R&D)经费支出的增长速度始终在增加
B. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长速度最快的年份是2017年
C. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长最多的年份是2017年
D. 2018年,基础研究经费约占该年研究与试验发展( (R&D)经费支出的10%
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
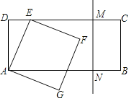
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,以
个单位的速度运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 也从
也从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,当经过________秒时.直线
个单位的速度运动,当经过________秒时.直线![]() 和正方形
和正方形![]() 开始有公共点?
开始有公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 y1=﹣2x2+2,直线 y2=2x+2,当 x 任取一值时,x 对应的函数值分别为 y1、y2.若 y1≠y2,取 y1、y2 中的较小值记为 M;若 y1=y2,记 M=y1=y2.例如;当 x=1 时,y1=0,y2=4,y1<y2, 此时 M=0,下列判断中正确的是( )

①当 x>0 时,y1>y2;②当 x<0 时,x 值越大,M 值越小;③使得 M 大于 2 的 x 值不存在;④使得 M=1 的 x 值是﹣![]() 或
或![]() .
.
A. ①②③ B. ①④ C. ②③④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AB=4,BC=2,点O在AB的延长线上,OB=![]() ,∠AOE=60°,动点P从点O出发,以每秒2个单位长度的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从B点出发,以每秒1个单位长度的速度沿折线B-C-D向点D运动,Q与D重合时,P,Q同时停止运动,设P的运动时间t秒.
,∠AOE=60°,动点P从点O出发,以每秒2个单位长度的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从B点出发,以每秒1个单位长度的速度沿折线B-C-D向点D运动,Q与D重合时,P,Q同时停止运动,设P的运动时间t秒.
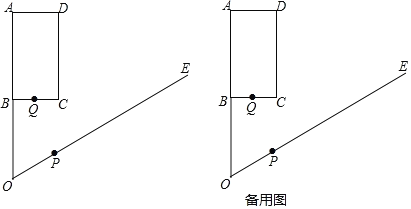
(1)∠BOC= ,PA的最小值是 ;
(2)当⊙P过点C时,求⊙P的劣弧与线段OA围成的封闭图形的面积;
(3)当⊙P与矩形ABCD的边所在直线相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
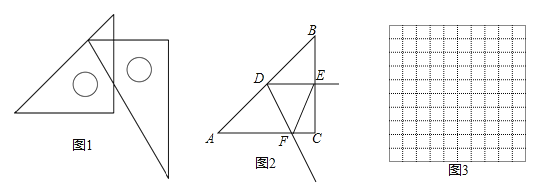
【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.
下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,我校将在周末举行“亲近大自然”的社会实践活动,现随机抽取了部分学生进行主题为“你最想去的景点是千鹤湖公园”的问卷调查,要求学生只能从“A(华中工委纪念馆),B(洋马菊花园),C(千鹤湖公园),D(丹顶鹤自然保护区)”四个景点中选择一项,根据调查结果,绘制了如图的两幅不完整的统计图:
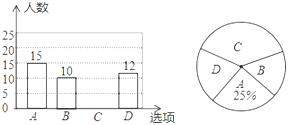
请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)在扇形统计图中,求B所占的圆心角度数;
(4)若该校有3600名学生,试估计该校最想去千鹤湖公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年的著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
(1)图中给出了七行数字,根据构成规律,第![]() 行中从左边数第
行中从左边数第![]() 个数是 ;
个数是 ;
(2)第![]() 行中从左边数第
行中从左边数第![]() 个数为 ;第
个数为 ;第![]() 行中所有数字之和为 .
行中所有数字之和为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com