Question

【题目】某市球类运动协会为了筹备一次大型体育活动，购进了一定数量的体育器材，器材管理员对购买的部分器材进行了统计，图表和图是器材管理员通过采集数据后，绘制的两幅不完整的频率分布表与频数分布直方图．请你根据图表中提供的信息，解答以下问题：

频率分布表
器材种类	频数	频率
排 球	20
乒乓球拍	50	0.50
篮 球	25	0.25
足 球
合 计		1

（1）填充频率分布表中的空格．
（2）在图中，将表示“排球”和“足球”的部分补充完整．
（3）若该协会购买这批体育器材时，篮球和足球一共花去950元，且足球每个的价格比篮球多10元，现根据筹备实际需要，准备再采购篮球和足球这两种球共10个（两种球的个数都不能为0），计划资金不超过320元，试问该协会有哪几种购买方案？

Answer 1

【答案】
（1）解：50÷0.50=100个；

则足球有100﹣20﹣50﹣25=5个；

足球频率 =0.05；

排球频率 =0.2；

合计为100．

故答案为：0.2； 5，0.05； 100

（2）解：如图：

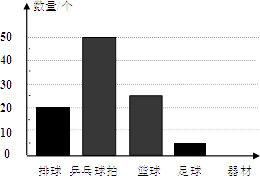
（3）解：设篮球每个x元，足球每个（x+10）元，列方程得，

25x+5（x+10）=950，

解得x=30，

则篮球每个30元，足球每个40元．

设再买y个篮球，列不等式得，

30y+40（10﹣y）≤320，

解得y≥8，

由于篮球足球共10个，

则篮球8个，足球2个；或篮球9个，足球1个

【解析】（1）根据乒乓球的总数为50，频数为0.50，求出体育器材总数，然后减去乒乓球、排球、篮球数目，即可得到足球频数、频率及合计数．（2）根据统计表中的数据，将统计图补充完整即可．（3）列方程求出篮球和足球的单价，再根据单价列出不等式，推知购买方案．
【考点精析】通过灵活运用一元一次不等式组的应用和频数分布直方图，掌握1、审：分析题意，找出不等关系；2、设：设未知数；3、列：列出不等式组；4、解：解不等式组；5、检验：从不等式组的解集中找出符合题意的答案；6、答：写出问题答案；特点：①易于显示各组的频数分布情况；②易于显示各组的频数差别．（注意区分条形统计图与频数分布直方图）即可以解答此题．