
分析 (1)利用周长减去AB和BC的长,即可求得AC;
(2)利用勾股定理的逆定理即可作出判断.
解答 解:(1)AC=12$\sqrt{5}$+4$\sqrt{15}$-$\sqrt{320}$-$\sqrt{80}$=12$\sqrt{5}$+4$\sqrt{15}$-8$\sqrt{5}$-4$\sqrt{5}$=4$\sqrt{15}$;
(2)∵($\sqrt{320}$)2=($\sqrt{80}$)2+(4$\sqrt{15}$)2,
∴AB2=BC2+AC2,
∴△ABC是直角三角形.
点评 本题主要考查了勾股定理的逆定理:用到的知识点是已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{12}$÷$\sqrt{3}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
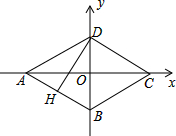 如图,四边形ABCD是菱形,对角线AC=8,BD=6,DH⊥AB于H.
如图,四边形ABCD是菱形,对角线AC=8,BD=6,DH⊥AB于H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
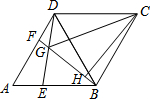 如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=a,BG=b,且a、b满足下列关系:a2+b2=5,ab=2,则GH=$\frac{3}{2}$.
如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=a,BG=b,且a、b满足下列关系:a2+b2=5,ab=2,则GH=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=0\\ y=0\end{array}$ | B. | $\left\{\begin{array}{l}x=-5\\ y=0\end{array}$ | C. | $\left\{\begin{array}{l}x=3\\ y=1\end{array}$ | D. | $\left\{\begin{array}{l}x=-1\\ y=3\end{array}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
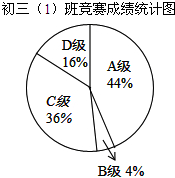 初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )
初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )| A. | B级人数比A级人数少21 | B. | 50人得分的众数是22 | ||
| C. | 50人得分的平均数是80 | D. | 50人得分的中位数是80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com