
【题目】如图,已知动点A在函数 ![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 . 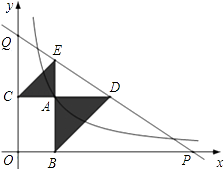
【答案】![]()
【解析】解: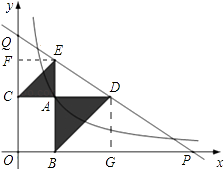
解法一:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.
令A(t, ![]() ),则AD=AB=DG=
),则AD=AB=DG= ![]() ,AE=AC=EF=t.
,AE=AC=EF=t.
在直角△ADE中,由勾股定理,得DE= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴QE= ![]() ,
,
∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴DP= ![]() .
.
又∵QE:DP=4:9,
∴ ![]() :
: ![]() =4:9,
=4:9,
解得t2= ![]() .
.
∴图中阴影部分的面积= ![]() AC2+
AC2+ ![]() AB2=
AB2= ![]() t2+
t2+ ![]() ×
× ![]() =
= ![]() +3=
+3= ![]() ;
;
解法二:∵QE:DP=4:9,
∴EF:PG=4:9,
设EF=4t,则PG=9t,
∴A(4t, ![]() ),
),
由AC=AE AD=AB,
∴AE=4t,AD= ![]() ,DG=
,DG= ![]() ,GP=9t,
,GP=9t,
∵△ADE∽△GPD,
∴AE:DG=AD:GP,
4t: ![]() =
= ![]() :9t,即t2=
:9t,即t2= ![]() ,
,
图中阴影部分的面积= ![]() ×4t×4t+
×4t×4t+ ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


科目:初中数学 来源: 题型:
【题目】直线y= ![]() x﹣2与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
x﹣2与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
(1)求抛物线的解析式;
(2)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,此时∠3=∠4.试判断AB与CD的位置关系,你是如何思考的?
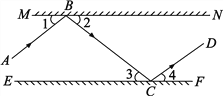
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地. 
(1)当n=200时,①根据信息填表:
A地 | B地 | C地 | 合计 | |
产品件数(件) | x | 2x | 200 | |
运费(元) | 30x |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE. 
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条总长为1860米的公路,在使用旧设备施工17天后,为尽快完成任务,工程队引进了新设备,从而将工作效率提高了50%,结果比原计划提前15天完成任务.
(1)工程队在使用新设备后每天能修路多少米?
(2)在使用旧设备和新设备工作效率不变的情况下,工程队计划使用旧设备m天,使用新设备n(16≤n≤26)天修建一条总长为1500米的公路,使用旧设备一天需花费16000元,使用新设备一天需花费25000元,当m、n分别为何值时,修建这条公路的总费用最少,并求出最少费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com