【题目】如图二次函数
的图象与y轴正半轴相交，其顶点坐标为（
）下列结论正确的是（ ）
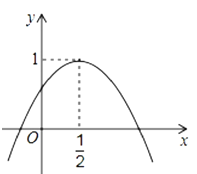
A. abc>0B. a=b
C. a=4c-4D. 方程
有两个不相等的实数根
应用题作业本系列答案科目：初中数学 来源： 题型：
【题目】企业举行“爱心一日捐”活动，捐款金额分为五个档次，分别是50元，100元，150元，200元，300元．宣传小组随机抽取部分捐款职工并统计了他们的捐款金额，绘制成两个不完整的统计图，请结合图表中的信息解答下列问题：
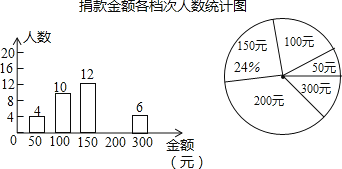
（1）宣传小组抽取的捐款人数为 人，请补全条形统计图；
（2）统计的捐款金额的中位数是 元；
（3）在扇形统计图中，求100元所对应扇形的圆心角的度数；
（4）已知该企业共有500人参与本次捐款，请你估计捐款总额大约为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
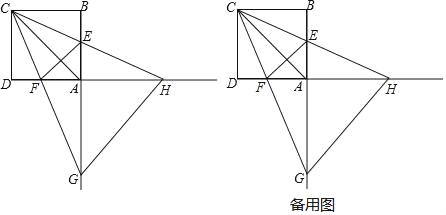
【题目】如图，正方形ABCD的边长为4，点E，F分别在边AB，AD上，且∠ECF＝45°，CF的延长线交BA的延长线于点G，CE的延长线交DA的延长线于点H，连接AC，EF．，GH．
（1）填空：∠AHC ∠ACG；（填“＞”或“＜”或“＝”）
（2）线段AC，AG，AH什么关系？请说明理由；
（3）设AE＝m，
①△AGH的面积S有变化吗？如果变化．请求出S与m的函数关系式；如果不变化，请求出定值．
②请直接写出使△CGH是等腰三角形的m值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况，从七、八年级各随机抽取50名学生进行测试，并对成绩（百分制）进行整理、描述和分析．部分信息如下：
a．七年级成绩频数分布直方图：
b．七年级成绩在
这一组的是：70 72 74 75 76 76 77 77 77 78 79
c．七、八年级成绩的平均数、中位数如下：
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息，回答下列问题：
（1）在这次测试中，七年级在80分以上（含80分）的有 人；
（2）表中m的值为 ；
（3）在这次测试中，七年级学生甲与八年级学生乙的成绩都是78分，请判断两位学生在各自年级的排名谁更靠前，并说明理由；
（4）该校七年级学生有400人，假设全部参加此次测试，请估计七年级成绩超过平均数76.9分的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为迎接十二运，某校开设了A：篮球，B：毽球，C：跳绳，D：健美操四种体育活动，为了解学生对这四种体育活动的喜欢情况，在全校范围内随机抽取若干名学生，进行问卷调查（每个被调查的同学必须选择而且只能在4中体育活动中选择一种）．将数据进行整理并绘制成以下两幅统计图（未画完整）．
（1）这次调查中，一共查了 名学生：
（2）请补全两幅统计图：
（3）若有3名最喜欢毽球运动的学生，1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动，欲从中选出2人担任组长（不分正副），求两人均是最喜欢毽球运动的学生的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】传统节日“端午节”的早晨，小文妈妈为小文准备了四个粽子作早点：一个枣馅粽，一个肉馅粽，两个花生馅粽，四个粽子除内部馅料不同外，其它一切均相同．
（1）小文吃前两个粽子刚好都是花生馅粽的概率为 ；
（2）若妈妈在早点中给小文再增加一个花生馅的粽子，则小文吃前两个粽子都是花生馅粽的可能性是否会增大？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知锐角∠AOB如图，（1）在射线OA上取一点C，以点O为圆心，OC长为半径作
，交射线OB于点D，连接CD；
（2）分别以点C，D为圆心，CD长为半径作弧，交于点M，N；
（3）连接OM，MN．
根据以上作图过程及所作图形，下列结论中错误的是（ ）
A. ∠COM=∠CODB. 若OM=MN，则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面的例题及点拨，并解决问题：
例题：如图①，在等边
中，
是
边上一点(不含端点
)，
是的外角
的平分线上一点，且
．求证：
．
点拨：如图②，作
，
与
的延长线相交于点
，得等边
，连接
．易证：
，可得
；又，则
，可得
；由
，进一步可得
又因为
，所以
，即：．
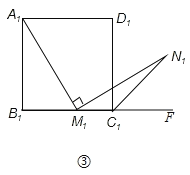
问题：如图③，在正方形
中，
是
边上一点(不含端点
)，
是正方形的外角
的平分线上一点，且
．求证：
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
