
【题目】如图,边长为![]() 的正方形
的正方形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,将正方形
,将正方形![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() ,则
,则![]()
![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
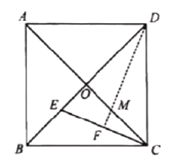
过点M作MP⊥CD垂足为P,过点O作OQ⊥CD垂足为Q,根据正方形的性质得到AB=AD=BC=CD=![]() ,∠DCB=∠COD=∠BOC=90°,根据折叠的性质得到∠EDF=∠CDF,设OM=PM=x,根据相似三角形的性质即可得到结论.
,∠DCB=∠COD=∠BOC=90°,根据折叠的性质得到∠EDF=∠CDF,设OM=PM=x,根据相似三角形的性质即可得到结论.
过点M作MP⊥CD垂足为P,过点O作OQ⊥CD垂足为Q,

∵ 正方形的边长为![]() ,
,
∴OD=1, OC=1, OQ=DQ=![]() ,由折叠可知,∠EDF=∠CDF.
,由折叠可知,∠EDF=∠CDF.
又∵AC⊥BD, ∴OM=PM,
设OM=PM=x
∵OQ⊥CD,MP⊥CD
∴∠OQC=∠MPC=900, ∠PCM=∠QCO,
∴△CMP∽△COQ
∴![]() , 即
, 即 , 解得x=
, 解得x=![]() -1
-1
∴OM=PM=![]() -1.
-1.
故选D


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
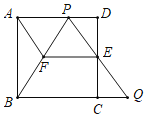
【题目】如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:![]() ;
;
(2)过点E作![]() 交PB于点F,连结AF,当
交PB于点F,连结AF,当![]() 时,①求证:四边形AFEP是平行四边形;
时,①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
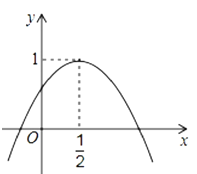
【题目】如图二次函数![]() 的图象与y轴正半轴相交,其顶点坐标为(
的图象与y轴正半轴相交,其顶点坐标为(![]() )下列结论正确的是( )
)下列结论正确的是( )
A. abc>0B. a=b
C. a=4c-4D. 方程![]() 有两个不相等的实数根
有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,![]() 的平分线交图形G于点D,连接AD,CD.
的平分线交图形G于点D,连接AD,CD.
(1)求证:AD=CD;
(2)过点D作DE![]() BA,垂足为E,作DF
BA,垂足为E,作DF![]() BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
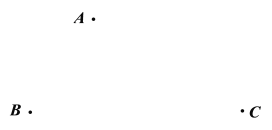
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程![]() (米)与时间
(米)与时间![]() (秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
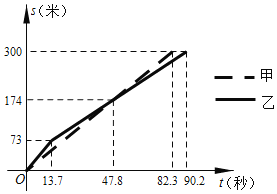
A. 乙队率先到达终点
B. 甲队比乙队多走了![]() 米
米
C. 在![]() 秒时,两队所走路程相等
秒时,两队所走路程相等
D. 从出发到![]() 秒的时间段内,乙队的速度慢
秒的时间段内,乙队的速度慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() ,角的两边分别交直线
,角的两边分别交直线![]() 于
于![]() 两点,设
两点,设![]() 点间的距离为
点间的距离为![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
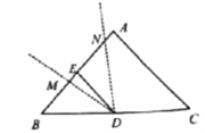
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是根据![]() 两点间的距离
两点间的距离![]() 进行取点、画图、测量,分别得到了 与 的几组对应值:
进行取点、画图、测量,分别得到了 与 的几组对应值:
| 0 | 0.30 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| 3.00 | 3.50 | 3.68 | 3.81 | 3.90 | 3.93 | 4.10 |
| 2.88 | 2.81 | 2.69 | 2.67 | 2.80 | 3.15 | 3.85 | 5.24 | 6.01 | 6.71 | 7.27 | 7.44 | 8.87 |
请你通过计算,补全表格
(2)描点、连线:在平面直角坐标系![]() 中,描出表中各组数值所对应的点
中,描出表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象:
的图象:

(3)探究性质:随着自变量![]() 的不断增大,函数
的不断增大,函数![]() 的变化趋势:
的变化趋势:
(4)解决问题:当![]() 时,
时,![]() 的长度大约是____
的长度大约是____![]() (保留两位小数).
(保留两位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示二次函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于
的图像交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,直线
的右侧,直线![]() 分别与
分别与![]() 、
、![]() 轴交于
轴交于![]() 、
、![]() 两点,其中
两点,其中![]() .
.
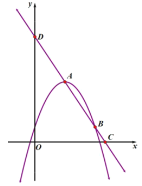
(1)求![]() 、
、![]() 两点的横坐标;
两点的横坐标;
(2)若![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的值;
的值;
(3)二次函数图像的对称轴与![]() 轴交于点
轴交于点![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
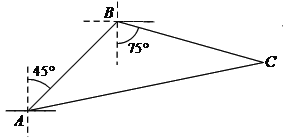
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,点O是对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,下列结论:
①图形中全等的三角形只有三对; ②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF=OA;⑤AE2+BE2=2OPOB.其中正确的个数有( )个.
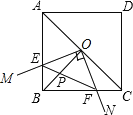
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com