
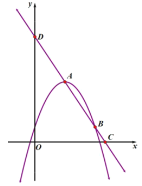
【题目】如图所示二次函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于
的图像交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,直线
的右侧,直线![]() 分别与
分别与![]() 、
、![]() 轴交于
轴交于![]() 、
、![]() 两点,其中
两点,其中![]() .
.
(1)求![]() 、
、![]() 两点的横坐标;
两点的横坐标;
(2)若![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的值;
的值;
(3)二次函数图像的对称轴与![]() 轴交于点
轴交于点![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)点![]() 、
、![]() 横坐标分别为
横坐标分别为![]() ,
,![]() ;(2)
;(2)![]() 的值为
的值为![]() 或
或![]() ;(3)存在,
;(3)存在,![]() 的值为
的值为![]() 或
或![]() ,见解析.
,见解析.
【解析】
(1)根据二次函数![]() 与一次函数
与一次函数![]() 相交,可列出一元二次方程,求得
相交,可列出一元二次方程,求得![]() 、
、![]() 坐标.
坐标.
(2)根据![]() 是以
是以![]() 为腰的等腰三角形,则
为腰的等腰三角形,则![]() 和
和![]() ,可列出含有
,可列出含有![]() 的方程并求解.
的方程并求解.
(3)分![]() 在
在![]() 轴上方和
轴上方和![]() 在
在![]() 轴下方两种情况,作辅助线,应用勾股定理等公式进行求解.
轴下方两种情况,作辅助线,应用勾股定理等公式进行求解.
(1)![]() 二次函数
二次函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于
的图像交于![]() 、
、![]() 两点,
两点,
![]() 联立
联立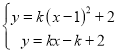 ,
,
解得:![]() 或
或![]() .
.
![]() 点
点![]() 在点
在点![]() 的右侧,
的右侧,
![]() 点
点![]() 、
、![]() 横坐标分别为
横坐标分别为![]() ,
,![]() .
.
(2)由(1)得点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,
故![]() ,
,![]() ,
,![]() .
.
![]() 若
若![]() 是以
是以![]() 为腰的等腰三角形
为腰的等腰三角形
![]() ①当
①当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() .
.
②当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() (舍)
(舍)
综上所述:![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.
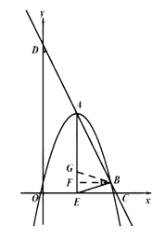
(3)存在.
①点![]() 在
在![]() 轴上方时,则
轴上方时,则![]() ,即
,即![]() 时,
时,
过点![]() 作
作![]() 点
点![]() ,在
,在![]() 上作点
上作点![]() ,使
,使![]() ,
,
![]() ,
,![]() 轴,
轴,
![]() 轴
轴
![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,
轴,![]() ,
,
![]() ,
,![]() .
.
![]() .
.
又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
解得:![]() ,
,![]() (舍)
(舍)
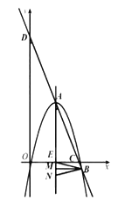
②点![]() 在
在![]() 轴下方时,则
轴下方时,则![]() 即
即![]() 时,
时,
过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,在
,在![]() 的延长线上作点
的延长线上作点![]() ,使
,使![]() .
.
![]() ,
,![]() 轴,
轴,
![]() 轴,
轴,![]() .
.
![]() ,
,
![]() .
.
![]() 轴,
轴,![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,![]() .
.
![]() .
.![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
解得:![]() ,
,![]() (舍).
(舍).
![]() 综上所述:存作实数
综上所述:存作实数![]() ,使得
,使得![]() ,
,![]() 的值为
的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
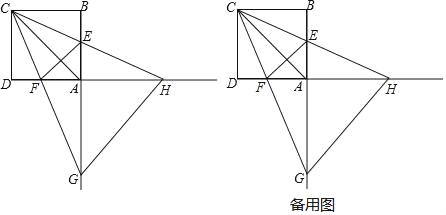
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中,有![]() 个红球,
个红球,![]() 个白球,这些球除颜色外都相同.
个白球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出![]() 个球,摸到红球的概率是________;
个球,摸到红球的概率是________;
(2)搅匀后先从中任意摸出![]() 个球(不放回),再从余下的球中任意摸出
个球(不放回),再从余下的球中任意摸出![]() 个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)
个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点![]() ,以线段
,以线段![]() 为直径作圆,圆心为
为直径作圆,圆心为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 轴上任意一动点,连接
轴上任意一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() :
:
①当![]() 时,求所有
时,求所有![]() 点的坐标 (直接写出);
点的坐标 (直接写出);
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
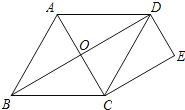
【题目】如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.
(1)求证:四边形DECO是矩形;
(2)连接AE交BD于点F,当∠ADB=30°,DE=2时,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边![]() 中,
中,![]() 是
是![]() 边上一点(不含端点
边上一点(不含端点![]() ),
),![]() 是
是![]() 的外角
的外角![]() 的平分线上一点,且
的平分线上一点,且![]() .求证:
.求证:![]() .
.

点拨:如图②,作![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,得等边
,得等边![]() ,连接
,连接![]() .易证:
.易证:![]() ,可得
,可得![]() ;又
;又![]() ,则
,则![]() ,可得
,可得![]() ;由
;由![]() ,进一步可得
,进一步可得![]() 又因为
又因为![]() ,所以
,所以![]() ,即:
,即:![]() .
.

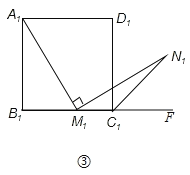
问题:如图③,在正方形![]() 中,
中,![]() 是
是![]() 边上一点(不含端点
边上一点(不含端点![]() ),
),![]() 是正方形
是正方形![]() 的外角
的外角![]() 的平分线上一点,且
的平分线上一点,且![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(1,5)和点B,与y轴相交于点C(0,6).
的图象相交于点A(1,5)和点B,与y轴相交于点C(0,6).
(1)求一次函数和反比例函数的解析式;
(2)现有一直线l与直线y=kx+b平行,且与反比例函数y=![]() 的图象在第一象限有且只有一个交点,求直线l的函数解析式.
的图象在第一象限有且只有一个交点,求直线l的函数解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com