
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() ,角的两边分别交直线
,角的两边分别交直线![]() 于
于![]() 两点,设
两点,设![]() 点间的距离为
点间的距离为![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
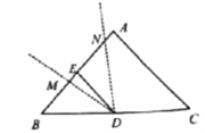
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是根据![]() 两点间的距离
两点间的距离![]() 进行取点、画图、测量,分别得到了 与 的几组对应值:
进行取点、画图、测量,分别得到了 与 的几组对应值:
| 0 | 0.30 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| 3.00 | 3.50 | 3.68 | 3.81 | 3.90 | 3.93 | 4.10 |
| 2.88 | 2.81 | 2.69 | 2.67 | 2.80 | 3.15 | 3.85 | 5.24 | 6.01 | 6.71 | 7.27 | 7.44 | 8.87 |
请你通过计算,补全表格
(2)描点、连线:在平面直角坐标系![]() 中,描出表中各组数值所对应的点
中,描出表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象:
的图象:

(3)探究性质:随着自变量![]() 的不断增大,函数
的不断增大,函数![]() 的变化趋势:
的变化趋势:
(4)解决问题:当![]() 时,
时,![]() 的长度大约是____
的长度大约是____![]() (保留两位小数).
(保留两位小数).
【答案】(1)![]() (2)详见解析(3)详见解析(4)
(2)详见解析(3)详见解析(4)![]()
【解析】
(1)①当x=BM=0时,当![]() 时,假设
时,假设![]() 交
交![]() 的延长线于点
的延长线于点![]() ,得出
,得出![]() 为
为![]() 的中位线,根据旋转性质
的中位线,根据旋转性质![]() ,即可解答
,即可解答
(2)描点出如下图象,从图象可以看出:随着自变量x的不断增大,函数y的变化趋势;
(3)观察函数图形可知当![]() 时,
时,![]() 随
随![]() 增大而减小,当
增大而减小,当![]() 时,
时,![]() 随
随![]() 增大而增大.
增大而增大.
(4)MN=2BM,设![]() ,得到
,得到![]() ,在证明
,在证明![]() ,得到
,得到![]() ,再利用
,再利用![]() 得到
得到![]() ,代入即可解答
,代入即可解答
(1)当![]() 时,
时,![]() 点与
点与![]() 点分别和
点分别和![]() 点、
点、![]() 点重合,
点重合,![]()
当![]() 时,假设
时,假设![]() 交
交![]() 的延长线于点
的延长线于点![]()
![]()
![]()
又![]() 为
为![]() 的中点
的中点![]()
![]() 为
为![]() 的中位线
的中位线
根据旋转性质
![]()
![]() (外角性质)
(外角性质)
![]()
![]()
![]()
![]()
![]()
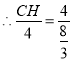
![]() 即
即![]() 点与
点与![]() 点重合
点重合
![]()
(2)根据表格描点可得:
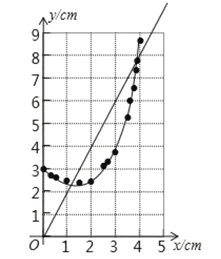
(3)根据图像可得:
当![]() 时,
时,![]() 随
随![]() 增大而减小,
增大而减小,
当![]() 时,
时,![]() 随
随![]() 增大而增大.
增大而增大.
(4)![]()
设![]()
![]()
![]() (外角性质)
(外角性质)
![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
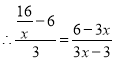
![]()
解得:![]()
所以![]() 的长度大约是4或
的长度大约是4或![]()


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
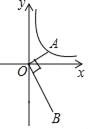
【题目】如图,已知点A是反比例函数y=![]() (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
A. y=﹣![]() B. y=
B. y=![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.
(1)小文吃前两个粽子刚好都是花生馅粽的概率为 ;
(2)若妈妈在早点中给小文再增加一个花生馅的粽子,则小文吃前两个粽子都是花生馅粽的可能性是否会增大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
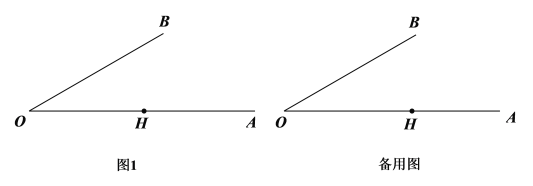
【题目】已知![]() ,H为射线OA上一定点,
,H为射线OA上一定点,![]() ,P为射线OB上一点,M为线段OH上一动点,连接PM,满足
,P为射线OB上一点,M为线段OH上一动点,连接PM,满足![]() 为钝角,以点P为中心,将线段PM顺时针旋转
为钝角,以点P为中心,将线段PM顺时针旋转![]() ,得到线段PN,连接ON.
,得到线段PN,连接ON.
(1)依题意补全图1;
(2)求证:![]() ;
;
(3)点M关于点H的对称点为Q,连接QP.写出一个OP的值,使得对于任意的点M总有ON=QP,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一张矩形纸片,按以下步骤进行操作:
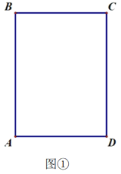
(Ⅰ)将矩形纸片沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上点
边上点![]() 处,如图②;
处,如图②;
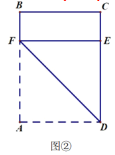
(Ⅱ)在第一次折叠的基础上,过点![]() 再次折叠,使得点
再次折叠,使得点![]() 落在边
落在边![]() 上点
上点![]() 处,如图③,两次折痕交于点
处,如图③,两次折痕交于点![]() ;
;
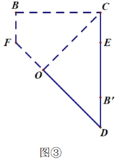
(Ⅲ)展开纸片,分别连接![]() 、
、![]() 、
、![]() 、
、![]() ,如图④.
,如图④.
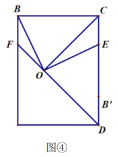
(探究)
(1)证明:![]() ;
;
(2)若![]() ,设
,设![]() 为
为![]() ,
,![]() 为
为![]() ,求
,求![]() 关于
关于![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点![]() ,以线段
,以线段![]() 为直径作圆,圆心为
为直径作圆,圆心为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 轴上任意一动点,连接
轴上任意一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() :
:
①当![]() 时,求所有
时,求所有![]() 点的坐标 (直接写出);
点的坐标 (直接写出);
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,点A、B、D、E在圆O上,弧AE=弧DE,连接BE交AE于F,∠BFC=45°,EF=2,BF=4.
(1)求AE的长;
(2)求证:BC是圆O的切线;
(3)求tan∠ABC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com