
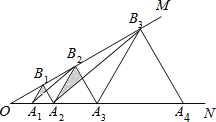
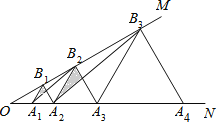
【题目】如图,已知![]() ,点
,点![]() 在射线
在射线![]() 上,点
上,点![]() …在射线
…在射线![]() 上,
上,![]() 、
、![]() 、
、![]() …均为等边三角形,分别连接
…均为等边三角形,分别连接![]() ,连接
,连接![]() ….若
….若![]() ,从左往右的阴影面积依次记作
,从左往右的阴影面积依次记作![]() .则
.则![]() =______.
=______.
【答案】![]()
【解析】
易证∠A1OB1=∠A1B1O=30°,从而可得B1A=OA1=a,同理可得A2B2=OA2=2a,B3A3=OA3=4a,…,从而归纳得到BnAn=2n-1a,即可得到S正△AnBnAn+1=![]() BnAn2=
BnAn2=![]() 4n-2a2.易证A1B1∥A2B2,从而可得△A1B1C1∽△B2A2C1,根据相似三角形的性质可得
4n-2a2.易证A1B1∥A2B2,从而可得△A1B1C1∽△B2A2C1,根据相似三角形的性质可得![]() =
=![]() =
=![]() ,根据合比性质可得
,根据合比性质可得![]() =
=![]() ,根据两个三角形高相等时面积比等于底的比可得S1=
,根据两个三角形高相等时面积比等于底的比可得S1=![]() S△A1B1A2,同理可得Sn=
S△A1B1A2,同理可得Sn=![]() S△AnBnAn+1,由此就可求出Sn.
S△AnBnAn+1,由此就可求出Sn.
∵△A1B1A2是等边三角形,∴∠B1A1A2=60°.
∵∠MON=30°,∴∠OB1A1=60°30°=30°,
∴∠A1OB1=∠A1B1O,∴B1A=OA1=a.
同理:A2B2=OA2=2a,B3A3=OA3=4a,…
BnAn=2n1a,
∴S正△AnBnAn+1=![]() BnAn2=
BnAn2=![]() (2n1a)2.
(2n1a)2.
=![]() 22n2a2=
22n2a2=![]() 4n1a2=
4n1a2=![]() 4n2a2
4n2a2
∵△A1B1A2、△A2B2A3为等边三角形,
∴∠B1A1A2=∠B2/span>A2A3=60°,
∴A1B1∥A2B2,
∴△A1B1C1∽△B2A2C1,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,即S1=
,即S1=![]() S△A1B1A2.
S△A1B1A2.
同理可得Sn=![]() S△AnBnAn+1=
S△AnBnAn+1=![]()
![]() 4n2a2=
4n2a2=![]()
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
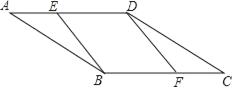
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() ,角的两边分别交直线
,角的两边分别交直线![]() 于
于![]() 两点,设
两点,设![]() 点间的距离为
点间的距离为![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
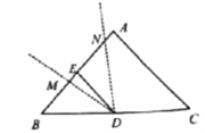
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是根据![]() 两点间的距离
两点间的距离![]() 进行取点、画图、测量,分别得到了 与 的几组对应值:
进行取点、画图、测量,分别得到了 与 的几组对应值:
| 0 | 0.30 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| 3.00 | 3.50 | 3.68 | 3.81 | 3.90 | 3.93 | 4.10 |
| 2.88 | 2.81 | 2.69 | 2.67 | 2.80 | 3.15 | 3.85 | 5.24 | 6.01 | 6.71 | 7.27 | 7.44 | 8.87 |
请你通过计算,补全表格
(2)描点、连线:在平面直角坐标系![]() 中,描出表中各组数值所对应的点
中,描出表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象:
的图象:

(3)探究性质:随着自变量![]() 的不断增大,函数
的不断增大,函数![]() 的变化趋势:
的变化趋势:
(4)解决问题:当![]() 时,
时,![]() 的长度大约是____
的长度大约是____![]() (保留两位小数).
(保留两位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
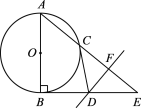
【题目】如图,在Rt△ABE中,∠B=90°,以AB为直径的⊙O交AE于点C,CE的垂直平分线FD交BE于D,连接CD.
(1)判断CD与⊙O的位置关系,并证明;
(2)若AC·AE=12,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
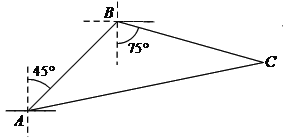
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解家长关注孩子成长方面的状况,某学校开展了针对家长的“您最关心孩子哪方面的成长”的主题调查,调查设置了“健康安全”,“日常学习”,“习惯养成”,“情感品质”四个项目,并随机抽取了部分家长进行调查,要求家长只能选择其中一个项目,根据调查结果绘制了如下两幅不完整的统计图.
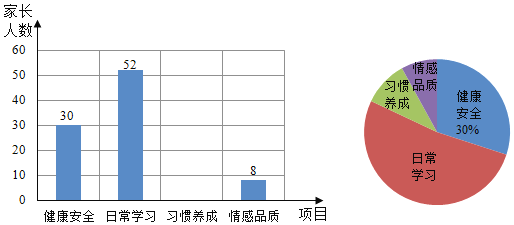
(1)本次调查共抽取了多少名学生家长?
(2)通过计算补全条形统计图;
(3)若全校共有2000名学生家长,估计有多少位学生家长最关心孩子“情感品质”方面的成长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1.
(2)平移△ABC,使点A移动到点A2(0,2),画出平移后的△A2B2C2并写出点B2、C2的坐标.
(3)在△ABC、△A1B1C1、△A2B2C2中,△A2B2C2与 成中心对称,其对称中心的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上的一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则下列结论中:
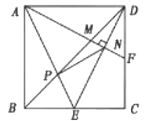
①![]() ;②
;②![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④
;④![]() 正确的是()
正确的是()
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com