
分析 (1)根据二次函数y=x2-(2k-1)x+k2+1的图象与x轴有两交点,得出x2-(2k-1)x+k2+1=0时,有两个不相等的实数根,从而可知△>0,解不等式即可得出答案;
(2)由根与系数关系得出方程,解方程即可得出答案.
解答 解:(1)∵二次函数y=x2-(2k-1)x+k2+1的图象与x轴有两交点,
∴当y=0时,x2-(2k-1)x+k2+1=0有两个不相等的实数根.
∴△=b2-4ac=[-(2k-1)]2-4×1×(k2+1)>0.
解得k<-$\frac{3}{4}$;
(2)当y=0时,x2-(2k-1)x+k2+1=0.
则x1+x2,=2k-1,x1•x2=k2+1,
∵$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{2k-1}{{k}^{2}+1}$=-$\frac{3}{2}$,
解得:k=-1或k=$\frac{1}{3}$(舍去),
∴k=-1.
点评 本题考查抛物线与x轴的交点、根与系数关系;解题关键是能将二次函数与一元二次方程建立关系,根据根的情况,可知△的值.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知⊙O的内接四边形ABCD,AD=$\sqrt{2}$,CD=1,半径为1,则∠B的度数为( )
如图,已知⊙O的内接四边形ABCD,AD=$\sqrt{2}$,CD=1,半径为1,则∠B的度数为( )| A. | 60° | B. | 70° | C. | 75° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
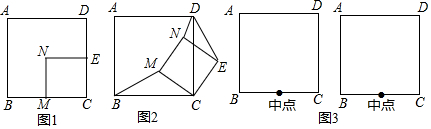
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图某防汛大堤的横断面为梯形ABCD,斜坡AB的坡度i1=1:1.5,斜坡CD的坡度i2=1:1,大堤顶高AD为10米,为了增强抗洪能力,现将大堤加高,加高部分的横截面为梯形ADFE,AD∥EF,且点E、F分别在BA、CD的延长线上,新坝顶宽EF为7.5米,求大堤加高了多少米?
如图某防汛大堤的横断面为梯形ABCD,斜坡AB的坡度i1=1:1.5,斜坡CD的坡度i2=1:1,大堤顶高AD为10米,为了增强抗洪能力,现将大堤加高,加高部分的横截面为梯形ADFE,AD∥EF,且点E、F分别在BA、CD的延长线上,新坝顶宽EF为7.5米,求大堤加高了多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E是正方形ABCD的CD边上的一点,BF⊥AE于F,
如图,E是正方形ABCD的CD边上的一点,BF⊥AE于F,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com