
 如图,E是正方形ABCD的CD边上的一点,BF⊥AE于F,
如图,E是正方形ABCD的CD边上的一点,BF⊥AE于F,分析 (1)根据两角相等的两个三角形相似,即可证明△ADE∽△BFA;
(2)利用三角形的面积比等于相似比的平方,即可解答.
解答 (1)证明:∵BF⊥AE于点F,四边形ABCD为正方形,
∴△ADE和△BFA均为直角三角形,
∵DC∥AB,
∴∠DEA=∠FAB,
∴△ADE∽△BFA;
(2)解:∵AD=2,E为CD的中点,
∴DE=1,
∴AE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴$\frac{AE}{AB}=\frac{\sqrt{5}}{2}$,
∵△ADE∽△BFA,
∴$\frac{{S}_{△BFA}}{{S}_{△ADE}}$=($\frac{2}{\sqrt{5}}$)2=$\frac{4}{5}$,
∵S△ADE=$\frac{1}{2}$×1×2=1,
∴S△BFA=$\frac{4}{5}$S△ADE=$\frac{4}{5}$.
点评 本题主要考查三角形相似的性质与判定,熟记相似三角形的判定是解决第(1)小题的关键;第(2)小题中,利用相似三角形的面积比是相似比的平方是解决此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
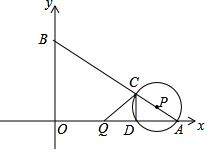 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D,连结CD、QC.
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D,连结CD、QC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查全国初中生的身体素质情况 | |
| B. | 调查一批蜡烛的使用寿命 | |
| C. | 调查一架“歼20”隐形战机各部零件的质量 | |
| D. | 调查我国2012年中央电视台春节联欢晚会的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△AOB绕点O逆时针方向旋转45°后得到△A′OB′,若∠AOB=10°,则∠AOB′的度数是( )
如图,将△AOB绕点O逆时针方向旋转45°后得到△A′OB′,若∠AOB=10°,则∠AOB′的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com