
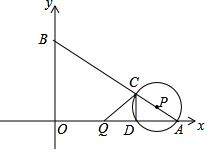
 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A��B������ֱ�Ϊ��8��0������0��6��������Q�ӵ�O������P�ӵ�Aͬʱ�������ֱ�����OA����AB�������1����λ����/����ٶ������˶����˶�ʱ��Ϊt���룩��0��t��5������PΪԲ�ģ�PA��Ϊ�뾶�ġ�P��AB��OA����һ������ֱ�Ϊ��C��D������CD��QC��
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A��B������ֱ�Ϊ��8��0������0��6��������Q�ӵ�O������P�ӵ�Aͬʱ�������ֱ�����OA����AB�������1����λ����/����ٶ������˶����˶�ʱ��Ϊt���룩��0��t��5������PΪԲ�ģ�PA��Ϊ�뾶�ġ�P��AB��OA����һ������ֱ�Ϊ��C��D������CD��QC������ ��1����CD��OB����$\frac{AD}{OA}$=$\frac{AC}{AB}$����$\frac{AD}{8}$=$\frac{2t}{10}$���Ƴ�AD=$\frac{8}{5}$t����D��Q�غ�ʱ��OQ+AD=8���ɵ÷���t+$\frac{8}{5}$t=8���ⷽ�̼��ɣ�
��2���������������ۢٵ�0��t��$\frac{40}{13}$ʱ����$\frac{40}{13}$��t��5ʱ���ֱ���⼴�ɣ�
��3����CQ���P����ʱ���ɡ�CDQ�ס�ADC����CD2=AD•QD���ɵã�$\frac{6}{5}$t��2=��8-t-$\frac{8}{5}$t��•$\frac{8}{5}$t�����t=$\frac{16}{7}$���۲�ͼ�ɽ�����⣬ע�⡰�߶�QC����
��� �⣺��1����Rt��AOB�У���OA=8��OB=6��
��AB=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��AC�ǡ�Pֱ����
���CDA=90�㣬����CD��OA��
��CD��OB��
��$\frac{AD}{OA}$=$\frac{AC}{AB}$=$\frac{CD}{BO}$��
��$\frac{AD}{8}$=$\frac{2t}{10}$=$\frac{CD}{6}$��
��AD=$\frac{8}{5}$t��CD=$\frac{6}{5}$t��
��OQ=t��
��D��Q�غ�ʱ��OQ+AD=8��
��t+$\frac{8}{5}$t=8��
��t=$\frac{40}{13}$��
��t=$\frac{40}{13}$sʱ��D��Q�غϣ�
��2���ٵ�0��t��$\frac{40}{13}$ʱ��S=$\frac{1}{2}$•��8-t-$\frac{8}{5}$t��•$\frac{6}{5}$t=-$\frac{39}{25}$t2+$\frac{24}{5}$t��
��$\frac{40}{13}$��t��5ʱ��s=$\frac{1}{2}$��t+$\frac{8}{5}$t-8��•$\frac{6}{5}$t=$\frac{39}{25}$t2-$\frac{24}{5}$t��
����������S=$\left\{\begin{array}{l}{-\frac{39}{25}{t}^{2}+\frac{24}{5}t}&{��0��t��\frac{40}{13}��}\\{\frac{39}{25}{t}^{2}-\frac{24}{5}t}&{��\frac{40}{13}��t��5��}\end{array}\right.$��
��3����CQ���P����ʱ���ɡ�CDQ�ס�ADC����CD2=AD•QD��
�ࣨ$\frac{6}{5}$t��2=��8-t-$\frac{8}{5}$t��•$\frac{8}{5}$t��
���t=$\frac{16}{7}$��
�۲�ͼ���֪��0��t$��\frac{16}{7}$��$\frac{40}{13}$��t��5ʱ����P���߶�QCֻ��һ�����㣮
���� ���⿼��Բ�ۺ��⡢���������ε��ж������ʡ�ƽ���߷��߶γɱ����������ֶκ�����֪ʶ������Ĺؼ���ѧ���÷������۵�˼��˼�����⣬ѧ��ȡ����λ�ý��ʵ�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪��O���ڽ��ı���ABCD��AD=$\sqrt{2}$��CD=1���뾶Ϊ1�����B�Ķ���Ϊ��������
��ͼ����֪��O���ڽ��ı���ABCD��AD=$\sqrt{2}$��CD=1���뾶Ϊ1�����B�Ķ���Ϊ��������| A�� | 60�� | B�� | 70�� | C�� | 75�� | D�� | 80�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼij��Ѵ��̵ĺ����Ϊ����ABCD��б��AB���¶�i1=1��1.5��б��CD���¶�i2=1��1����̶���ADΪ10�ף�Ϊ����ǿ�����������ֽ���̼Ӹߣ��Ӹ߲��ֵĺ����Ϊ����ADFE��AD��EF���ҵ�E��F�ֱ���BA��CD���ӳ����ϣ��°Ӷ���EFΪ7.5�ף����̼Ӹ��˶����ף�
��ͼij��Ѵ��̵ĺ����Ϊ����ABCD��б��AB���¶�i1=1��1.5��б��CD���¶�i2=1��1����̶���ADΪ10�ף�Ϊ����ǿ�����������ֽ���̼Ӹߣ��Ӹ߲��ֵĺ����Ϊ����ADFE��AD��EF���ҵ�E��F�ֱ���BA��CD���ӳ����ϣ��°Ӷ���EFΪ7.5�ף����̼Ӹ��˶����ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12�������4������ | B�� | 10�������10������ | ||
| C�� | 4�������2������ | D�� | 10�������5������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��E��������ABCD��CD���ϵ�һ�㣬BF��AE��F��
��ͼ��E��������ABCD��CD���ϵ�һ�㣬BF��AE��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com