
【题目】如图,已知![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() ,半径
,半径![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,点
,点![]() 的对应点为
的对应点为![]() ,当点
,当点![]() 与点
与点![]() 重合时停止.连接
重合时停止.连接![]() 并延长到点
并延长到点![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() ______;
______;
(2)如图,当点![]() 与点
与点![]() 重合时,判断
重合时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
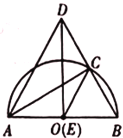
(3)如图,当![]() 时,求
时,求![]() 的长;
的长;

(4)如图,若点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,当
,当![]() 与半圆
与半圆![]() 相切时,直接写出直线
相切时,直接写出直线![]() 与
与![]() 的位置关系.
的位置关系.

【答案】(1)![]() ;(2)
;(2)![]() 是等边三角形,理由见解析;(3)
是等边三角形,理由见解析;(3)![]() 的长为
的长为![]() 或
或![]() ;(4)
;(4)![]()
【解析】
(1)先证AC垂直平分DB,即可证得AD=AB;
(2)先证AD=BD,又因为AD=AB,可得△ABD是等边三角形;
(3)分当点![]() 在
在![]() 上时和当点
上时和当点![]() 在
在![]() 上时,由勾股定理列方程求解即可;
上时,由勾股定理列方程求解即可;
(4)连结OC,证明OC∥AD, 由![]() 与半圆
与半圆![]() 相切,可得∠OCP=90°,即可得到
相切,可得∠OCP=90°,即可得到![]() 与
与![]() 的位置关系.
的位置关系.
解:(1)∵![]() 为直径,
为直径,
∴∠ACB=90°,
又∵![]()
∴AD=AB
∴![]() ,
,
故答案为10;
(2)![]() 是等边三角形,
是等边三角形,
理由如下:∵点![]() 与点
与点![]() 重合,∴
重合,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() 是等边三角形;
是等边三角形;
(3)∵![]() ,∴
,∴![]() ,
,
当点![]() 在
在![]() 上时,
上时,
则![]() ,
,![]() ,∵
,∵![]() ,
,![]() ,
,
∴在![]() 和
和![]() 中,
中,
由勾股定理得![]() ,即
,即![]() ,
,
解得![]() ,∴
,∴![]() ;
;
当点![]() 在
在![]() 上时,同理可得
上时,同理可得![]() ,
,
解得![]() ,∴
,∴![]() ,
,
综上所述,![]() 的长为
的长为![]() 或
或![]() ;
;
(4)![]() .
.
如图,连结OC,
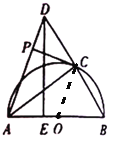
∵![]() 与半圆
与半圆![]() 相切,
相切,
∴OC⊥PC,
∵△ADB为等腰三角形,![]() ,
,
∴∠DAC=∠BAC,
∵AO=OC
∴∠CAO=∠ACO,
∴∠DAC=∠ACO,
∴OC∥AD,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
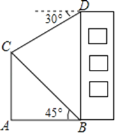
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
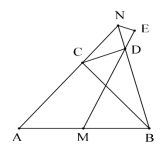
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列6×6的网格中,横、纵坐标均A(0,3),B(5,3)、C(1,5)都是格点在网格中仅用无刻度的直尺作图,保留作图痕迹.
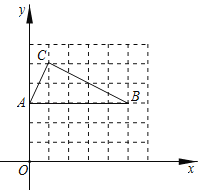
(1)画出以AB为斜边的等腰Rt△ABD(D在AB下方);
(2)连接CD交AB于点E,则∠ACE的度数为 ;
(3)在直线AB下方找一个格点F,连接CF,使∠ACF=∠AEC,直接写出F点坐标 ;
(4)由上述作图直接写出tan∠AEC的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() 、
、![]() 、
、![]() .
.
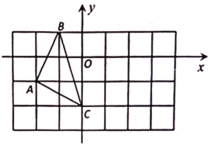
(1)点![]() 关于坐标原点
关于坐标原点![]() 对称的点的坐标为______;
对称的点的坐标为______;
(2)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后得到的
,画出旋转后得到的![]() ;
;
(3)在(2)中,求边![]() 所扫过区域的面积是多少?(结果保留
所扫过区域的面积是多少?(结果保留![]() ).
).
(4)若![]() 、
、![]() 、
、![]() 三点的横坐标都加3,纵坐标不变,图形
三点的横坐标都加3,纵坐标不变,图形![]() 的位置发生怎样的变化?
的位置发生怎样的变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:如图①,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() .线段
.线段![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的中线.
的中线.
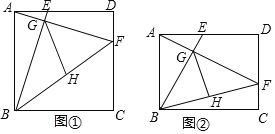
(1)求证:![]() .
.
(2)判断线段![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
问题拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() .若
.若![]() 是
是![]() 的中线,则线段
的中线,则线段![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数图象的顶点是![]() ,且与
,且与![]() 轴的交点的纵坐标为4.
轴的交点的纵坐标为4.
(1)求这个二次函数的表达式;
(2)当![]() 取哪些值时,
取哪些值时,![]() 的值随
的值随![]() 值的增大而增大?
值的增大而增大?
(3)点![]() 在这个二次函数的图象上吗?
在这个二次函数的图象上吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
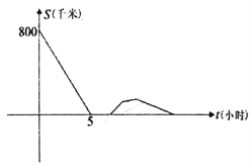
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车相遇后都停下来休息,快车休息2个小时后,以原速的![]() 继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的
继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的![]() 返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.
返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的对角线BD经过坐标原点O,矩形的边分别平行于坐标轴,点A在函数![]() (
(![]() ≠0,
≠0,![]() <0)的图象上,点C的坐标为(2,
<0)的图象上,点C的坐标为(2,![]() ),则
),则![]() 的值为( )
的值为( )
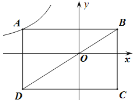
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com