
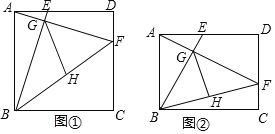
【题目】问题探究:如图①,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() .线段
.线段![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的中线.
的中线.
(1)求证:![]() .
.
(2)判断线段![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
问题拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() .若
.若![]() 是
是![]() 的中线,则线段
的中线,则线段![]() 的长为 .
的长为 .
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】为了减少雾霾的侵状,某市环保局与市委各部门协商,要求市民在春节期间禁止燃放烟花爆竹,为了征集市民对禁燃的意见,政府办公室进行了抽样调查,调查意见表设计为:“满意““一般””无所谓””反对”四个选项,调查结果汇总制成如下不完整的统计图,请根据提供的信息解答下面的问题.
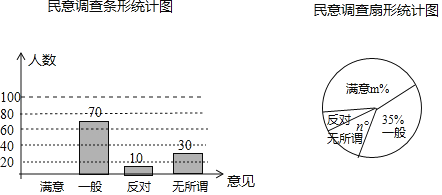
(1)参与问卷调查的人数为 .
(2)扇形统计图中的m= ,n= .补全条形统计图;
(3)若本市春节期间留守市区的市民有32000人,请你估计他们中持“反对”意见的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形 ABCD 内接于⊙O,连接 AC、BD,∠BAD+2∠ACB=180°.
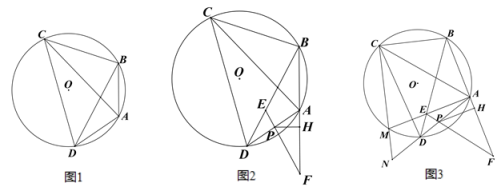
(1)如图 1,求证:点 A 为弧 BD 的中点;
(2)如图 2,点 E 为弦 BD 上一点,延长 BA 至点 F,使得 AF=AB,连接 FE 交 AD 于点 P,过点 P 作 PH⊥AF 于点 H,AF=2AH+AP,求证:AH:AB=PE:BE;
(3)在(2)的条件下,如图 3,连接 AE,并延长 AE 交⊙O 于点 M,连接 CM,并延长 CM 交 AD 的延长线于点 N,连接 FD,∠MND=∠MED,DF=12﹒sin∠ACB,MN=![]() ,求 AH 的长.
,求 AH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() ,半径
,半径![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,点
,点![]() 的对应点为
的对应点为![]() ,当点
,当点![]() 与点
与点![]() 重合时停止.连接
重合时停止.连接![]() 并延长到点
并延长到点![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() ______;
______;
(2)如图,当点![]() 与点
与点![]() 重合时,判断
重合时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
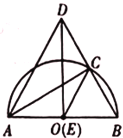
(3)如图,当![]() 时,求
时,求![]() 的长;
的长;

(4)如图,若点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,当
,当![]() 与半圆
与半圆![]() 相切时,直接写出直线
相切时,直接写出直线![]() 与
与![]() 的位置关系.
的位置关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
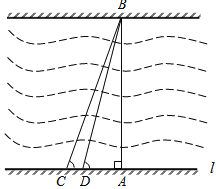
【题目】某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求:AB的长(精确到0.1米,参考数据:sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5).
查看答案和解析>>
科目:初中数学 来源: 题型:
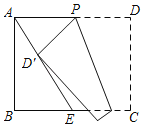
【题目】如图,在矩形ABCD中,AB=4,BC=6,E是BC的中点,连接AE,P是边AD上一动点,沿过点P的直线将矩形折叠,使点D落在AE上的点D′处,当△APD′是直角三角形时,PD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
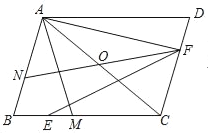
【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)若BM=4,MC=3,AC=![]() ,求AM的长度;
,求AM的长度;
(2)若∠ACB=45°,求证:AN+AF=![]() EF.
EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
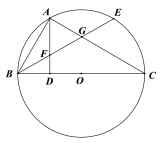
【题目】如图,BC是⊙O的直径,点A在⊙上,AD⊥BC,垂足为D,![]() ,BE分别交AD、AC与点F、G.
,BE分别交AD、AC与点F、G.
(1)证明:FA=FB.
(2)BD=DO=2,求弧EC的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com