
分析 先根据y轴上点的坐标特征求出A点坐标,再确定B点坐标,然后利用待定系数法求一次函数解析式.
解答 解:当x=0时,y=-2x-1=-1,则A(0,-1),
因为n2=9,
所以n=-3或3,
而点B位于x轴下方,
则n=-3,即B(3,-3),
把A(0,-1),B(3,-3)分别代入y=kx+b得$\left\{\begin{array}{l}{b=-1}\\{3k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=-1}\end{array}\right.$,
所以这个一次函数解析式为y=-$\frac{2}{3}$x-1.
点评 本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )| A. | 3 | B. | $\frac{20}{3}$ | C. | 1 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
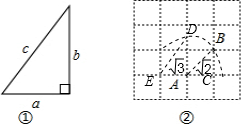
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
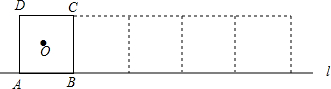
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com