
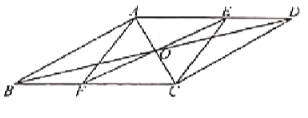
【题目】如图,在![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点,连接
上任意一点,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() ,
,![]() ,
,![]() .求出
.求出![]() 的边
的边![]() 上的高
上的高![]() 的值.
的值.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据平行四边形性质得BO=DO,AO=CO,AD∥BC,构造条件证△AOE≌△COF(ASA),证CF=AE,CF∥AE,即可;
(2)作AH⊥BC,根据直角三角形性质得CH=![]() ,再运用勾股定理可得.
,再运用勾股定理可得.
证明:(1)∵在ABCD中,AC,BD交于点O,
∴BO=DO,AO=CO,AD∥BC,
∴∠OAE=∠OCF,
在△AOE和△COF中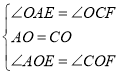 ,
,
∴△AOE≌△COF(ASA),
∴CF=AE,
∵CF∥AE,
∴四边形AFCE是平行四边形.
(2)作AH⊥BC,
因为四边形![]() 是平行四边形,
是平行四边形,
所以AD∥BC,
所以∠DAH=∠AHC=90°,
因为![]() ,
,
所以∠CAH=30°,
所以CH=![]()
所以AH=![]()
所以![]() 的边
的边![]() 上的高
上的高![]() 的值是
的值是![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( )
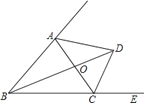
A. ∠BAC=70° B. ∠DOC=90° C. ∠BDC=35° D. ∠DAC=55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调査结果绘制了如下尚不完整的统计图:

根据以上信息解答下列问题:
(1)这次接受调查的市民总人数是_______人;
(2)扇形统计图中,“电视”所对应的圆心角的度数是_________;
(3)请补全条形统计图;
(4)若该市约有80万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是( )

A. 64° B. 62° C. 58° D. 52°
查看答案和解析>>
科目:初中数学 来源: 题型:
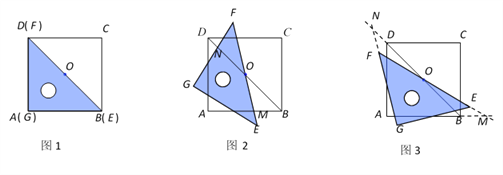
【题目】如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB,AC=4,求DE的长.
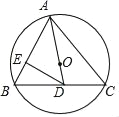
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )
A. 2+![]() B.
B. ![]() C. 2+
C. 2+![]() 或2-
或2-![]() D. 4+2
D. 4+2![]() 或2-
或2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在△ABC中,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,连接AM、AN.
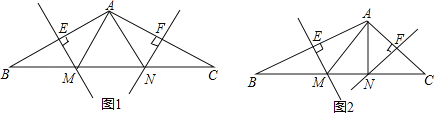
(1)求证:△AMN的周长=BC;
(2)若AB=AC,∠BAC=120°,试判断△AMN的形状,并证明你的结论;
(3)若∠C=45°,AC=3![]() ,BC=9,如图2所示,求MN的长.
,BC=9,如图2所示,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E、F在BC上,且CF=BE,连接DE,过点F作FG⊥AB于点G.

(1)如图1,若∠B=60°,DE平分∠ADC,且 ![]() ,
,![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
(2)点H在GF上,且HE=HF,延长EH交AC,CD于点O,Q,连接AQ,若AC=BC=EQ,∠EQC=45°,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com