
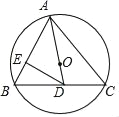
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB,AC=4,求DE的长.
【答案】(1)见解析;(2)2.
【解析】
(1)如图1中,延长AD交⊙O于点F,连接BF.首先证明∠ABF=90°,再证明∠AFB=∠C即可解决问题.
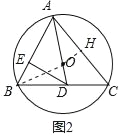
(2)如图2中,过点O作OH⊥AC于H,连接BO.想办法证明△BDE≌△AOH即可解决问题.
(1)证明:延长AD交⊙O于点F,连接BF.

∵AF为⊙O的直径,
∴∠ABF=90°,
∴∠AFB+∠BAD=90°,
∵∠AFB=∠ACB,
∴∠ACB+∠BAD=90°.
(2)证明:如图2中,过点O作OH⊥AC于H,连接BO.
∵∠AOB=2∠ACB,
∠ADC=2∠ACB,
∴∠AOB=∠ADC,
∴∠BOD=∠BDO,
∴BD=BO,
∴BD=OA,
∵∠BED=∠AHO,∠ABD=∠AOH,
∴△BDE≌△AOH,(AAS),
∴DE=AH,
∵OH⊥AC,
∴AH=CH=![]() AC,
AC,
∴AC=2DE=4,
∴DE=2.


科目:初中数学 来源: 题型:
【题目】某商场第一次用![]() 元购进某款机器人进行销售,很快销售一空,商家又用
元购进某款机器人进行销售,很快销售一空,商家又用![]() 元第二次购进同款机器人,所购进数量是第一次的
元第二次购进同款机器人,所购进数量是第一次的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.
元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于![]() 不考虑其他因素
不考虑其他因素![]() ,那么每个机器人的标价至少是多少元?
,那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
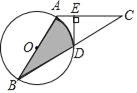
【题目】如图,AB是⊙O的直径,C是⊙O外一点,AB=AC,连接BC,交⊙O于点D,过点D作DE⊥AC,垂足为E.
(1)求证:DE与⊙O相切.
(2)若∠B=30°,AB=4,则图中阴影部分的面积是 (结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
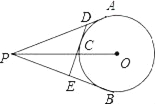
【题目】如图,PA、PB切⊙O于A、B,点C在弧AB上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现任意三个连续的整数中,最大数与最小数这两个数的平方差是4的倍数;
验证:(1) ![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续的整数中间的一个为n,计算最大数与最小数这两个数的平方差,并说明它是4的倍数;
延伸:说明任意三个连续的奇数中,最大的数与最小的数这两个数的平方差是8的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
①2a+b=0;
②当﹣1≤x≤3时,y<0;
③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )

A. ①②④ B. ①②③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
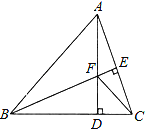
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①所有锐角三角函数值都为正数;②解直角三角形时只需已知除直角外的两个元素;③Rt△ABC中,∠B=90°,则sin2A+cos2A=1;④Rt△ABC中,∠A=90°,则tanCsinC=cosC.其中正确的命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com