
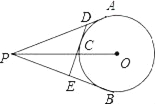
【题目】如图,PA、PB切⊙O于A、B,点C在弧AB上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是_____.
科目:初中数学 来源: 题型:
【题目】八年级(1)班从学校出发去某景点旅游,全班分成甲、乙两组,甲组乘坐大型客车,乙组乘坐小型客车.已知甲组比乙组先出发,汽车行驶的路程![]() (单位:
(单位:![]() )和行驶时间
)和行驶时间![]() (单位:
(单位:![]() )之间的函数关系如图所示.
)之间的函数关系如图所示.
根据图象信息,回答下列问题:
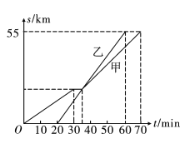
(1)学校到景点的路程为_ ,甲组比乙组先出发 , 组先到达旅游景点;
(2)求乙组乘坐的小型客车的平均速度;
(3)从图象中你还能获得哪些信息? (请写出一条)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
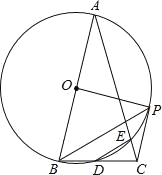
【题目】如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是( )

A. 64° B. 62° C. 58° D. 52°
查看答案和解析>>
科目:初中数学 来源: 题型:
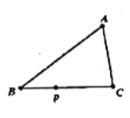
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以2
以2![]() 的速度运动,设运动时间为
的速度运动,设运动时间为![]()
![]() ,当
,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() 或12或4C.
或12或4C.![]() 或
或![]() 或12D.
或12D.![]() 或12或4
或12或4
查看答案和解析>>
科目:初中数学 来源: 题型:
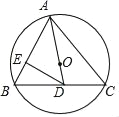
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB,AC=4,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
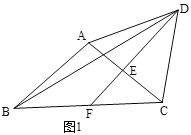
【题目】在△ABC中,AB=AC,在△ABC的外部作等边三角形△ACD,E为AC的中点,连接DE并延长交BC于点F,连接BD.
(1)如图1,若∠BAC=100°,则∠ABD的度数为_____,∠BDF的度数为______;
(2)如图2,∠ACB的平分线交AB于点M,交EF于点N,连接BN,若BN=DN,∠ACB=![]() .
.
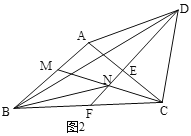
(I)用![]() 表示∠BAD;
表示∠BAD;
(II)①求证:∠ABN=30°;
②直接写出![]() 的度数以及△BMN的形状.
的度数以及△BMN的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
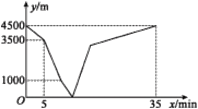
【题目】小宁和弟弟小强分别从家和图书馆出发,沿同一条笔直的马路相向而行.小宁先出发5分钟后,小强骑自行车匀速回家.小宁开始跑步中途改为步行,且步行的速度为跑步速度的一半,到达图书馆恰好用了35分钟.两人之间的距离y(m)与小宁离开出发地的时间x(min)之间的函数图象如图所示.则当弟弟到家时,小宁离图书馆的距离为___________米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com