
����Ŀ��ij�̳��ס��ҡ�������ҵ��Ա5���µ����۶��λ����Ԫ�����±���
�·� | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
�� | 7.2 | 9.6 | 9.6 | 7.8 | 9.3 |
�� | 5.8 | 9.7 | 9.8 | 5.8 | 9.9 |
�� | 4 | 6.2 | 8.5 | 9.9 | 9.9 |
��1�������ϱ��е����ݣ����±�����������
ͳ��ֵ | ƽ��������Ԫ�� | ��λ������Ԫ�� | ��������Ԫ�� |
�� | 9.3 | 9.6 | |
�� | 8.2 | 5.8 | |
�� | 7.7 | 8.5 |
��2���ס��ҡ�������ҵ��Ա��˵�Լ�������ҵ���ã�����ͬ˭��˵������˵�����ɣ�
���𰸡�
��1��8.7,9.7,9.9
��2���⣺����ͬ��˵������ƽ�����۶���ҡ������ߣ�
���������⣺��1�� ![]() =
= ![]() ��7.2+9.6+9.6+7.8+9.3��=8.7����Ԫ��
��7.2+9.6+9.6+7.8+9.3��=8.7����Ԫ��
���Ұ��մ�С�����������У��ɵ�5.8��5.8��9.7��9.8��9.9��
��λ��Ϊ9.7��Ԫ��
���г��ִ���������Ϊ9.9��Ԫ��
���Դ��ǣ�8.7��9.7��9.9��
�����㾫����������Ŀ����֪��������������ƽ��������λ�������������֪ʶ���Եõ�����Ĵ𰸣���Ҫ�������������ܷ���=ƽ����������ؼ��Ǹ�����֪����ȷ���������Լ��������Ӧ���ܷ�������λ����Ψһ�ģ��������ݵ�����λ���йأ������ܳ�������������ݣ���������һ����Ҳ���ܶ������һ�������������е�����


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���E.F�ֱ���AB��CD�ϣ�AE=CF������AF��BF��DE��CE���ֱ���H��G.
��֤��(1)�ı���AECF��ƽ���ı��Ρ�(2)EF��GH����ƽ�֡�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����ֱ�����������(��ABC�����С�ACB��90��)��������һ�����ڣ���������A��B��C�ֱ����ڰ����ڱ��ϣ���֪��ADE����BED��90�㣬���AD��5cm��BE��7cm���������������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У����κ���y=�� ![]() x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��
x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��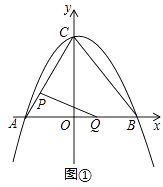
��1����գ�b= �� c=��
��2���ڵ�P��Q�˶������У���APQ������ֱ������������˵�����ɣ�
��3����x���·����ö��κ�����ͼ�����Ƿ���ڵ�M��ʹ��PQM���Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ������ڣ�������˶�ʱ��t���������ڣ���˵�����ɣ�
��4����ͼ�ڣ���N������Ϊ���� ![]() ��0�����߶�PQ���е�ΪH������NH������Q����ֱ��NH�ĶԳƵ�Q��ǡ�������߶�BC��ʱ����ֱ��д����Q������꣮
��0�����߶�PQ���е�ΪH������NH������Q����ֱ��NH�ĶԳƵ�Q��ǡ�������߶�BC��ʱ����ֱ��д����Q������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������x�ύ�ڵ��A����1��0���͵�B��4��0������y�ύ�ڵ�C��0��2����
��1���������߽���ʽ��
��2����P��������BC����һ�㣬PD��BC��PE��y�ᣬ�ֱ�BC�ڵ�D��E����DE= ![]() ʱ�����P�����ꣻ
ʱ�����P�����ꣻ
��3��M��ƽ����һ�㣬�����ϣ�2�������µġ�PDE�Ƶ�M����ʱ�뷽����ת90���P��D��E�Ķ�Ӧ��ֱ���P�䡢D�䡢E�䣮��P��E����е�ΪN����������ͬʱ����D����Nʱ�����D��ĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ס������Ӿ�����һ��һ�ȵ������۱����������ڱ���ʱ��·��![]() ��
��![]() ��ʱ��
��ʱ��![]() ����
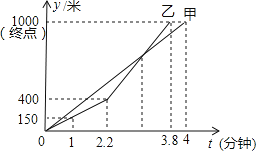
����![]() ֮��ĺ�����ϵͼ����ͼ��ʾ���������ͼ�ش��������⣺
֮��ĺ�����ϵͼ����ͼ��ʾ���������ͼ�ش��������⣺
![]() �����������ȫ����______ �ף�______ ���ȵ����յ㣻
�����������ȫ����______ �ף�______ ���ȵ����յ㣻
![]() �����������ʱ�ҵ��ٶȣ�
�����������ʱ�ҵ��ٶȣ�
![]() ������Ҷ��������֮ǰ�����Ǻ�ʱ���100�ף�
������Ҷ��������֮ǰ�����Ǻ�ʱ���100�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�A(-1,5)��B����1��0����C����4��3����
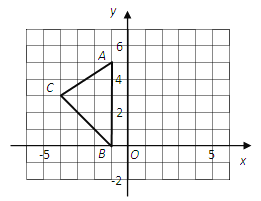
��1����ABC������� ��
��2������ͼ�л�����ABC����ƽ��2����λ������ƽ��5����λ��ġ�A1B1C1��
��3��д����A1��B1��C1�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ͼ����ͼ��ʾ���������½���������x=0ʱ������ֵ���������0��x��2ʱ������y��x���������С������x��0ʱ������y��x�������������������0��a��1����x=aʱ������ֵΪ0��������ȷ�Ľ�����(����)

A. �٢� B. �ڢ� C. �ۢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��ʦ�ڿ��������һ�����⣺��ͨ��̽��֪����![]() ��1.414�������Ǹ�����ѭ��С����Ҳ������������������������1����ô��˭��˵������С�������Ƕ�������С�����ֻش�����С������������ȫ��д��������������
��1.414�������Ǹ�����ѭ��С����Ҳ������������������������1����ô��˭��˵������С�������Ƕ�������С�����ֻش�����С������������ȫ��д��������������![]() ��1����ʾ����С�����֣�����ʦ�佱С����������϶�������˵�������������С����˵�����
��1����ʾ����С�����֣�����ʦ�佱С����������϶�������˵�������������С����˵�����
��1��![]() ����������a��
����������a��![]() ������������b����a+2b��
������������b����a+2b��![]() ��ֵ��
��ֵ��
��2����֪6+![]() =x+y������x��һ��������0��y��1����2x+��y��
=x+y������x��һ��������0��y��1����2x+��y��![]() ��2018��ֵ��
��2018��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com