
| A. | a-1、a+1、$\sqrt{1+{a}^{2}}$ | B. | 3(a-1)、4(a-1)、5(a-1) | C. | a-1、a、a+1 | D. | a+2、a、$\sqrt{2{a}^{2}+4}$ |
分析 由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解答 解:A、(a-1)2+($\sqrt{1+{a}^{2}}$)2≠(a+1)2,故不是直角三角形,故此选项错误;
B、[3(a-1)]2+[4(a-1)]2=[5(a-1)]2,故是直角三角形,故此选项正确;
C、(a-1)2+a2≠(a+1)2,故不是直角三角形,故此选项错误;
D、(a+2)2+a2≠($\sqrt{2{a}^{2}+4}$)2,故不是直角三角形,故此选项错误;
故选:B.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
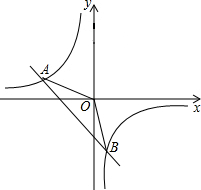 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.
已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${x^2}+\sqrt{5}x+1=0$ | B. | $\sqrt{2}x+1=0$ | C. | $\sqrt{x+1}+\sqrt{2}=0$ | D. | $\sqrt{a-1}$+2x=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}-\sqrt{3}$=3 | B. | 2$\sqrt{3}+3\sqrt{3}=5\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{5}+\frac{3\sqrt{2}}{5}=\sqrt{5}$ | D. | 3$\sqrt{6}-6\sqrt{6}=3\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
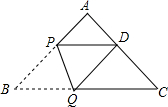 如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为2或2$\sqrt{2}$-2.
如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为2或2$\sqrt{2}$-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com