
【题目】如图,把长方形纸片![]() 沿
沿![]() 折叠后,使得点
折叠后,使得点![]() 与点
与点![]() 重合,点
重合,点![]() 落在点
落在点![]() 的位置上.
的位置上.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)证明见解析;(3)22. 5
;(2)证明见解析;(3)22. 5
【解析】
(1)根据矩形的性质和平行线的性质可得∠2=∠1=60°,然后根据折叠的性质可得∠BEF=∠2=60°,从而求出∠3的度数;
(2)根据矩形的性质和平行线的性质可得∠2=∠1,然后根据折叠的性质可得∠BEF=∠2,从而证出:∠BEF=∠1,最后根据等角对等边即可证出![]() ;
;
(3)过点E作EG⊥BC于G,根据平行线之间的距离处处相等即可求出:EG=AB=6,由折叠的性质,可设BE=ED=x,则AE=12-x,然后根据勾股定理列出方程,即可求出x的值,根据(2)的结论即可求出BF从而求出![]() 的面积.
的面积.
解:(1)∵四边形ABCD是长方形
∴AD∥BC
∴∠2=∠1=60°
由折叠可知:∠BEF=∠2=60°
∴∠3=180°-∠BEF-∠2=60°
(2)∵四边形ABCD是长方形
∴AD∥BC
∴∠2=∠1
由折叠可知:∠BEF=∠2
∴∠BEF=∠1
∴![]()
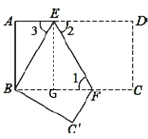
(3)过点E作EG⊥BC于G,如下图所示,
∴EG=AB=6
由折叠的性质,可设BE=ED=x,则AE=12-x
根据勾股定理:![]()
∴![]()
解得:x=7.5
∴![]()
∴![]()


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】一次函数![]() ,下列结论错误的是( )
,下列结论错误的是( )
A.若两点A(![]() ),B(
),B(![]() )在该函数图象上,且
)在该函数图象上,且![]() ,则
,则![]()
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得到![]() 的图象
的图象
D.函数的图象与![]() 轴的交点坐标是(0,4)
轴的交点坐标是(0,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示),如果大正方形的面积是64,小正方形的面积为4,直角三角形的两直角边长分别为a,b,且a> b . 那么下列结论:(1)a2+b2=64,(2)a-b=2,(3)ab=30,(4)a+b=2![]() .正确结论的个数有( )
.正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
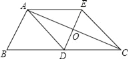
【题目】如图.在△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作与DE∥AB,DE与AC、AE分别交于点O、E,连接EC.
(1)求证:AD=EC;
(2)当△ABC满足 时,四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(3,2),B(4,3),C(1,1).

(1)在图中作出△ABC关于y轴对称的△![]()
![]()
![]() ;
;
(2)写出点△![]() ,
,![]() ,
,![]() 的坐标(直接写答案):
的坐标(直接写答案): ![]() ___;
___;![]() ___;
___;![]() ___;
___;
(3)△![]()
![]()
![]() 的面积为___;
的面积为___;
(4)在y轴上画出点P,使PB+PC最小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①b2﹣4ac>0;
②4a﹣2b+c<0;
③3b+2c<0;
④m(am+b)<a﹣b(m≠﹣1),
其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
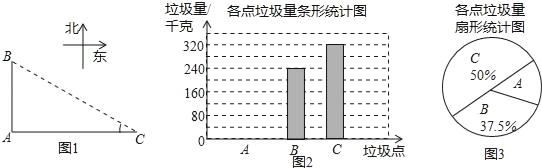
【题目】如图,A、B、C是三个垃圾存放点,点B、C分别位于点A的正北和正东方向,AC=200米,编号为1﹣6号的6名同学分别测得∠C的度数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | |
∠C(单位:度) | 37 | 36 | 37 | 40 | 34 | 38 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图,如图:
(1)求表中∠C度数的平均数,众数和中位数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=![]() (x>0)的图象经过点D.
(x>0)的图象经过点D.
(1)求点D的坐标及反比例函数的解析式;
(2)经过点C的一次函数y=kx+b(k≠0)的图象与反比例函数的图象交于P点,当k>0时,确定点P横坐标的取值范围(不必写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线与x轴的交点坐标分别为A(1,0),B(x2,0)(点B在点A的右侧),其对称轴是x=3,该函数有最小值是﹣2.
(1)求二次函数解析式;
(2)在图1上作平行于x轴的直线,交抛物线于C(x3,y3),D(x4,y4),求x3+x4的值;
(3)将(1)中函数的部分图象(x>x2)向下翻折与原图象未翻折的部分组成图象“G”,如图2,在(2)中平行于x轴的直线取点E(x5,y5)、(x4<x5),结合函数图象求x3+x4+x5的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com