
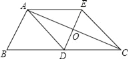
【题目】如图.在△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作与DE∥AB,DE与AC、AE分别交于点O、E,连接EC.
(1)求证:AD=EC;
(2)当△ABC满足 时,四边形ADCE是菱形.
【答案】(1)见解析;(2)∠BAC=90°.
【解析】
(1)首先证明四边形ABDE是平行四边形,可得AE=BD,再根据DC=DB可得AE=DC,进而证出四边形ADCE是平行四边形,可得AD=EC;(2)当∠BAC=90°时,可证出AD=DC,再根据有一组邻边相等的平行四边形是菱形可得四边形ADCE是菱形.
证明:(1)∵DE∥AB,AE∥BC,
∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD
又∵AD是BC边的中线,
∴BD=CD,
∴AE=CD,
∵AE∥CD,
∴四边形ADCE是平行四边形,
∴AD=EC;
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD=CD,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
故答案为∠BAC=90°.


科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题:
例题:已知关于x的多项式x2-4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得:x2-4x+m=(x+3)(x+n),则x2-4x+m=x2+(n+3)x+3n,
∴![]() ,解得:n =-7,m =-21.
,解得:n =-7,m =-21.![]()
∴另一个因式为(x-7),m的值为-21.
问题:仿照以上方法解答下面问题:
(1)已知关于x的多项式2x2+3x-k有一个因式是(x+4),求另一个因式以及k的值.
(2)已知关于x的多项式2x3+5x2-x+b有一个因式为(x+2),求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
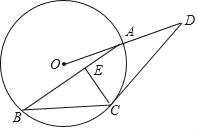
【题目】如图,已知点A,B,C在半径为4的⊙O上,过点C作⊙O的切线交OA的延长线于点D.
(Ⅰ)若∠ABC=29°,求∠D的大小;
(Ⅱ)若∠D=30°,∠BAO=15°,作CE⊥AB于点E,求:
①BE的长;
②四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了从甲、乙两名学生中选派一名学生参加市综合知识技能竞赛,对他们进 行了 8 次综合知识技能测试,记录如下:
学生 | 8 次测试成绩(分) | 平均数 | 中位数 | 方差 | |||||||
甲 | 95 | 82 | 88 | 81 | 93 | 79 | 84 | 78 | 85 | 35.5 | |
乙 | 83 | 92 | 80 | 95 | 90 | 80 | 85 | 75 | 84 | ||
(1)请你通过计算求出表格中所缺少的甲、乙两名学生这 8 次测试成绩的平均数、中位数 和方差;
(2)现要从中选派一人参加市综合知识技能竞赛,你认为选派哪名同学参加合适,请说明 理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下三个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°.其中结论正确的结论是()

A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与A.E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,一定成立的有________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,3)、B(3,-1),利用图中的“格点”完成下列作图并解答:

(1)在第三象限内找“格点”C,使得CA=CB,则点C的坐标是 ;
(2)在(1)的基础上,标出“格点”D,使得△DCB≌△ABC,则点D的坐标是 ;
(3)点M是x轴上一点,且MA-MB的值最大,则点M的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com