
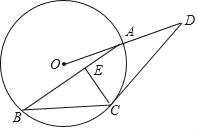
【题目】如图,已知点A,B,C在半径为4的⊙O上,过点C作⊙O的切线交OA的延长线于点D.
(Ⅰ)若∠ABC=29°,求∠D的大小;
(Ⅱ)若∠D=30°,∠BAO=15°,作CE⊥AB于点E,求:
①BE的长;
②四边形ABCD的面积.
【答案】(1)∠D=32°;(2)①BE=![]() ;②
;②![]()
【解析】
(Ⅰ)连接OC, CD为切线,根据切线的性质可得∠OCD=90°,根据圆周角定理可得∠AOC=2∠ABC=29°×2=58°,根据直角三角形的性质可得∠D的大小.
(Ⅱ)①根据∠D=30°,得到∠DOC=60°,根据∠BAO=15°,可以得出∠AOB=150°,进而证明△OBC为等腰直角三角形,根据等腰直角三角形的性质得出![]()
根据圆周角定理得出![]() 根据含
根据含![]() 角的直角三角形的性质即可求出BE的长;
角的直角三角形的性质即可求出BE的长;
②根据四边形ABCD的面积=S△OBC+S△OCD﹣S△OAB进行计算即可.
(Ⅰ)连接OC,
∵CD为切线,
∴OC⊥CD,
∴∠OCD=90°,
∵∠AOC=2∠ABC=29°×2=58°,
∴∠D=90°﹣58°=32°;
(Ⅱ)①连接OB,
在Rt△OCD中,∵∠D=30°,
∴∠DOC=60°,![]()
∵∠BAO=15°,
∴∠OBA=15°,
∴∠AOB=150°,
∴∠OBC=150°﹣60°=90°,
∴△OBC为等腰直角三角形,
∴![]()
∵![]()
在Rt△CBE中,![]()
∴![]()
②作BH⊥OA于H,如图,
∵∠BOH=180°﹣∠AOB=30°,
∴![]()
∴四边形ABCD的面积=S△OBC+S△OCD﹣S△OAB
![]()


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() ,下列结论错误的是( )
,下列结论错误的是( )
A.若两点A(![]() ),B(
),B(![]() )在该函数图象上,且
)在该函数图象上,且![]() ,则
,则![]()
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得到![]() 的图象
的图象
D.函数的图象与![]() 轴的交点坐标是(0,4)
轴的交点坐标是(0,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xoy中,直线y=![]() x+
x+![]() 交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l,将直线l绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).
交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l,将直线l绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).

(1)当直线l与直线y=![]() x+
x+![]() 平行时,求出直线l的解析式;
平行时,求出直线l的解析式;
(2)若直线l经过点A,①求线段AC的长;②直接写出旋转角α的度数;
(3)若直线l在旋转过程中与y轴交于D点,当△ABD、△ACD、△BCD均为等腰三角形时,直接写出符合条件的旋转角α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示),如果大正方形的面积是64,小正方形的面积为4,直角三角形的两直角边长分别为a,b,且a> b . 那么下列结论:(1)a2+b2=64,(2)a-b=2,(3)ab=30,(4)a+b=2![]() .正确结论的个数有( )
.正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
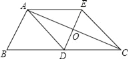
【题目】如图.在△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作与DE∥AB,DE与AC、AE分别交于点O、E,连接EC.
(1)求证:AD=EC;
(2)当△ABC满足 时,四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=![]() (x>0)的图象经过点D.
(x>0)的图象经过点D.
(1)求点D的坐标及反比例函数的解析式;
(2)经过点C的一次函数y=kx+b(k≠0)的图象与反比例函数的图象交于P点,当k>0时,确定点P横坐标的取值范围(不必写出过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com