
【题目】抛物线![]() 过点
过点![]() 和
和![]() ,点P为x轴正半轴上的一个动点,连接AP,在AP右侧作
,点P为x轴正半轴上的一个动点,连接AP,在AP右侧作![]() ,且
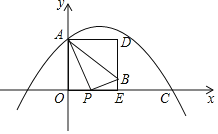
,且![]() ,点B经过矩形AOED的边DE所在的直线,设点P横坐标为t.
,点B经过矩形AOED的边DE所在的直线,设点P横坐标为t.
![]() 求抛物线解析式;
求抛物线解析式;
![]() 当点D落在抛物线上时,求点P的坐标;
当点D落在抛物线上时,求点P的坐标;
![]() 若以A、B、D为顶点的三角形与
若以A、B、D为顶点的三角形与![]() 相似,请直接写出此时t的值.
相似,请直接写出此时t的值.
【答案】(1)抛物线的解析式为:![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 、
、![]() 时,以A、B、D为顶点的三角形与
时,以A、B、D为顶点的三角形与![]() 相似.
相似.
【解析】
![]() 将
将![]() 、
、![]() 两点坐标代入抛物线
两点坐标代入抛物线![]() ,运用待定系数法即可求得解析式,然后根据对称轴公式求得即可;
,运用待定系数法即可求得解析式,然后根据对称轴公式求得即可;
![]() 先求得
先求得![]() 的坐标,进而求出点
的坐标,进而求出点![]() 的坐标,然后将
的坐标,然后将![]() 代入
代入![]() 中求出的抛物线的解析式,即可求出
中求出的抛物线的解析式,即可求出![]() 的值;
的值;
![]() 由于
由于![]() 时,点
时,点![]() 与点
与点![]() 重合,
重合,![]() 不存在,所以分
不存在,所以分![]() 和
和![]() 两种情况进行讨论,在每一种情况下,当以A、B、D为顶点的三角形与
两种情况进行讨论,在每一种情况下,当以A、B、D为顶点的三角形与![]() 相似时,即:以A、B、D为顶点的三角形与
相似时,即:以A、B、D为顶点的三角形与![]() 相似,进而又分两种情况:
相似,进而又分两种情况:![]() ∽
∽![]() 与
与![]() ∽
∽![]() ,根据相似三角形对应边的比相等列出比例式,求解即可.
,根据相似三角形对应边的比相等列出比例式,求解即可.
解:![]() 由题意得
由题意得 ,
,
解得![]() .
.
故抛物线的解析式为:![]() ;
;
![]() ,
,
![]() ,
,
易证,![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
假设![]() 在抛物线上,有
在抛物线上,有![]() ,
,
解得![]() 或
或![]() ,
,
![]() ,
,
![]() ,
,
即当![]() 时,点D落在抛物线上.
时,点D落在抛物线上.
![]() 当
当![]() 时,如图1,
时,如图1,
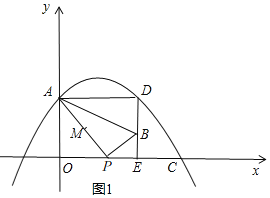
![]() ,
,,
![]() ,
,![]() ,
,
若![]() ∽
∽![]() ,
,
![]() ∽
∽![]()
![]() ∽
∽![]() ,
,
![]() ,即
,即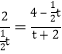 ,
,
化简得![]() ,此时t无解.
,此时t无解.
若![]() ∽
∽![]() ,
,
![]() ∽
∽![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,即
,即![]() ,化简得:
,化简得:![]() ,
,
解得:![]() .
.
![]() ,
,
![]() .
.
![]() 当
当![]() 时,如图2,
时,如图2,
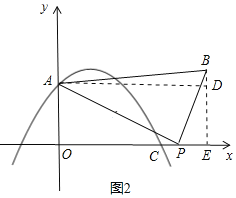
若![]() ∽
∽![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,即
,即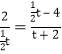 ,
,
化简得,![]() ,
,
解得![]() 负根舍去
负根舍去![]() .
.
![]() ∽
∽![]() ,
,
![]() ∽
∽![]() ,同理,此时t无解.
,同理,此时t无解.
综合上述:当![]() 、
、![]() 时,以A、B、D为顶点的三角形与
时,以A、B、D为顶点的三角形与![]() 相似.
相似.


科目:初中数学 来源: 题型:
【题目】如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
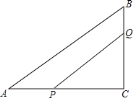
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发向点
点出发向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点出发向点
点出发向点![]() 以
以![]() 的速度移动,当其中一点首先到达终点时运动停止,若
的速度移动,当其中一点首先到达终点时运动停止,若![]() 、
、![]() 分别同时从
分别同时从![]() ,
,![]() 出发,几秒后四边形
出发,几秒后四边形![]() 是
是![]() 面积的
面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求证:无论m为任何实数,此函数图象与x轴总有两个交点;
(2)若此函数图象与x轴的一个交点为(-3,0),求此函数图象与x轴的另一个交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的对角线BD上一点,并且AD=DE,过点E作EF⊥BD交AB于点F.
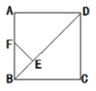
(1)求证:AF=BE,(2)若正方形的边长为1,求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP是∠ABC的平分线,AP⊥BP于P,连接PC,若△ABC的面积为1cm2则△PBC的面积为( ).
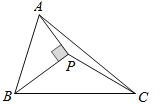
A. 0.4 cm2B. 0.5 cm2
C. 0.6 cm2D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接到一批生产帐篷订单后,开始组织甲、乙两车间同时开工.如图所示,两个车间连续工作了![]() ,甲车间因机器出故障,中途停工一段时间,然后按停工前的效率继续工作,直到与乙车间同时完成这批帐篷的加工任务为止.设甲、乙两个车间各自加工帐篷的数量为y(顶),乙车间加工的时间为
,甲车间因机器出故障,中途停工一段时间,然后按停工前的效率继续工作,直到与乙车间同时完成这批帐篷的加工任务为止.设甲、乙两个车间各自加工帐篷的数量为y(顶),乙车间加工的时间为![]() ,
,![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
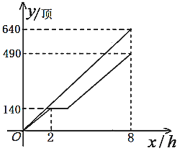
(1)乙车间每小时加工帐篷______顶,这批帐篷的总数为______顶;
(2)求甲车间维修设备后,甲车间加工帐篷数量![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求甲、乙两车间共同加工完成980顶帐篷时,乙车间所用的时间;
(4)在乙车间工作______![]() 时,乙车间比甲车间多生产120顶帐篷.
时,乙车间比甲车间多生产120顶帐篷.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com