
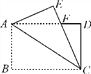
【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于_________.
【答案】![]()
【解析】分析:根据折叠的性质得到AE=AB,∠E=∠B=90°,易证Rt△AEF≌Rt△CDF,即可得到结论EF=DF;易得FC=FA,设FA=x,则FC=x,FD=6﹣x.在Rt△CDF中利用勾股定理得到关于x的方程x2=42+(6﹣x)2,解方程求出x,即可得到结论.
详解:∵矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,∴AE=AB,∠E=∠B=90°.
又∵四边形ABCD为矩形,∴AB=CD,∴AE=DC,而∠AFE=∠DFC.
在△AEF与△CDF中,∵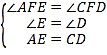 ,∴△AEF≌△CDF(AAS),∴EF=DF;
,∴△AEF≌△CDF(AAS),∴EF=DF;
∵四边形ABCD为矩形,∴AD=BC=6,CD=AB=4.
∵Rt△AEF≌Rt△CDF,∴FC=FA,设FA=x,则FC=x,FD=6﹣x.在Rt△CDF中,CF2=CD2+DF2,即x2=42+(6﹣x)2,解得:x=![]() ,则FD=6﹣x=
,则FD=6﹣x=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如下(未完成),解答下列问题:(1)若A组的频数比B组小24,求频数分布直方图中a= ,b= ;(2)扇形统计图中n= ,并补全频数分布直方图;
(3)若成绩在80分以上优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?
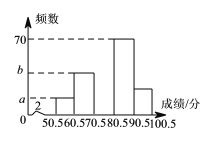
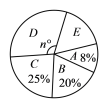
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)中自变量x和函数值y的部分对应值如下表:
x | … | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| … |
y | … | ﹣ | ﹣2 | ﹣ | ﹣2 | ﹣ | 0 |
| … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,﹣2);
③抛物线的对称轴是:x=1;
④在对称轴左侧,y随x增大而增大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
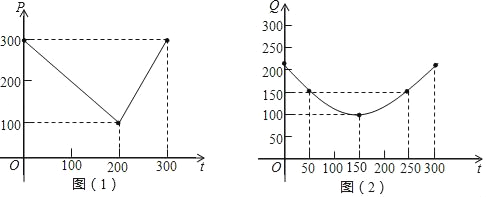
【题目】(7分)某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段Q=![]() (t﹣150)2+100 (0≤t≤300)表示,(注:市场售价和种植成本的单位:元/100kg,时间单位:天)
(t﹣150)2+100 (0≤t≤300)表示,(注:市场售价和种植成本的单位:元/100kg,时间单位:天)
(1)写出图(1)表示的市场售价P与时间t的函数关系式;
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 过点
过点![]() 和
和![]() ,点P为x轴正半轴上的一个动点,连接AP,在AP右侧作
,点P为x轴正半轴上的一个动点,连接AP,在AP右侧作![]() ,且
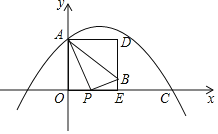
,且![]() ,点B经过矩形AOED的边DE所在的直线,设点P横坐标为t.
,点B经过矩形AOED的边DE所在的直线,设点P横坐标为t.
![]() 求抛物线解析式;
求抛物线解析式;
![]() 当点D落在抛物线上时,求点P的坐标;
当点D落在抛物线上时,求点P的坐标;
![]() 若以A、B、D为顶点的三角形与
若以A、B、D为顶点的三角形与![]() 相似,请直接写出此时t的值.
相似,请直接写出此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是![]() 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).
的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).

A.2.5B.2C.1.5D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的顶点坐标分别为A(2,3)、B (1,1)、C(2,1)
的顶点坐标分别为A(2,3)、B (1,1)、C(2,1)

(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出点
,并写出点![]() 的坐标为_________
的坐标为_________
(2)将![]() 向左平移4个单位长度得到
向左平移4个单位长度得到![]() ,直接写出点
,直接写出点![]() 的坐标为_________
的坐标为_________
(3)直接写出点B关于直线n(直线n上各点的纵坐标都为-1)对称点B'的坐标为________
(4)在![]() 轴上找一点P,使PA+PB的值最小,标出P点的位置(保留画图痕迹)
轴上找一点P,使PA+PB的值最小,标出P点的位置(保留画图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两组算式,解答问题:
第一组:![]() =2,
=2,![]() =2,
=2,![]() 、
、![]() ,
,![]() =0
=0
第二组:![]() =2,
=2,![]() =3,
=3,![]() =9,
=9,![]() =16,
=16,![]() =0
=0
(1)由第一组可得结论:对于任意实数a,![]() =_____.
=_____.
(2)由第二组可得结论:当a≥0时,![]() =_____.
=_____.
(3)利用(1)和(2)的结论计算:![]() =_____,
=_____,![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣3,4),(﹣3,1)若直线y=﹣2x+b与线段AB有公共点,则b的值可以为_____(写出一个即可)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com