
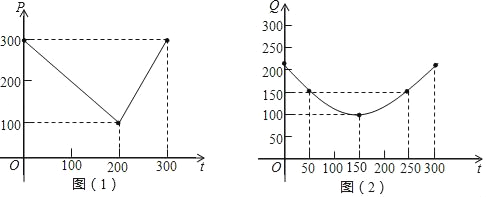
����Ŀ����7�֣�ij�߲˻�����ֲ���������������г������֪����2��1�����300���ڣ��������г��ۼ�������ʱ��Ĺ�ϵ��ͼ��1����һ�����߱�ʾ������������ֲ�ɱ�������ʱ��Ĺ�ϵ��ͼ��2���������߶�Q=![]() ��t��150��2+100 ��0��t��300����ʾ����ע���г��ۼۺ���ֲ�ɱ��ĵ�λ��Ԫ/100kg��ʱ�䵥λ���죩
��t��150��2+100 ��0��t��300����ʾ����ע���г��ۼۺ���ֲ�ɱ��ĵ�λ��Ԫ/100kg��ʱ�䵥λ���죩
��1��д��ͼ��1����ʾ���г��ۼ�P��ʱ��t�ĺ�����ϵʽ��
��2���϶��г��ۼۼ�ȥ��ֲ�ɱ�Ϊ�����棬�ʺ�ʱ���е����������������
���𰸡���1��P=![]() ����2���Ӷ���һ�տ�ʼ�ĵ�50�����д��������
����2���Ӷ���һ�տ�ʼ�ĵ�50�����д��������
��������
�ɴ�����=����-�ɱ�, ��ϴӶ���һ�����300����, �������г��ۼ�P������ʱ��t�����ϵ P=![]() ,����������ֲ�ɱ�Q������ʱ��t�����ϵQ=
,����������ֲ�ɱ�Q������ʱ��t�����ϵQ=![]() ��t��150��2+100(0��t��300), �����õ�������h(t) �Ľ���ʽ, ���ݷֶκ����ֶδ�����ԭ��, ���Ƿֱ���������Ϻ�������ֵ, �ۺ����۽��, ���ɵõ�����.
��t��150��2+100(0��t��300), �����õ�������h(t) �Ľ���ʽ, ���ݷֶκ����ֶδ�����ԭ��, ���Ƿֱ���������Ϻ�������ֵ, �ۺ����۽��, ���ɵõ�����.
��1����0��t��200ʱ�����г��ۼ�P��ʱ��t�ĺ�����ϵʽΪP=k1t+b1��
![]() ����
����![]() ��
��
����0��t��200ʱ���г��ۼ�P��ʱ��t�ĺ�����ϵʽΪP=��t+300��
��200��t��300ʱ�����г��ۼ�P��ʱ��t�ĺ�����ϵʽΪP=k2t+b2��
![]() ����
����![]() ��
��
����200��t��300ʱ���г��ۼ�P��ʱ��t�ĺ�����ϵʽΪP=2t��300��
���Ͽɵã�P=![]() ��
��
��2�����t��Ĵ�����ΪyԪ��
y=P��Q��
��0��t��200ʱ��y=����t+300����[![]() ��t��150��2+100]=
��t��150��2+100]=![]() ��
��
����t=50ʱ��yȡ�����ֵ����ʱy=100��
��200��t��300ʱ��y=��2t��300����[![]() ��t��150��2+100]=
��t��150��2+100]=![]() ��
��
��t=300ʱ��yȡ�����ֵ����ʱy=87.5��
���Ͽɵã��Ӷ���һ�տ�ʼ�ĵ�50�����д��������


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC����ADE�У�AB=AC����BAC=120�㣬��ADE=90�㣬��DAE=60�㣬FΪBC�е㣬����BE��DF��G��H�ֱ�ΪBE��DF���е㣬����GH��
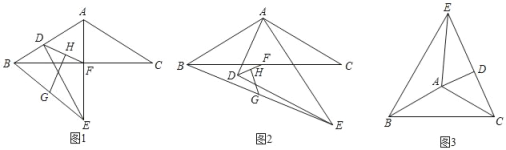
��1����ͼ1����D����ABC�ı�AB��ʱ����ֱ��д���߶�GH��HF��λ�ù�ϵ�� ����![]() =�� ����
=�� ����
��2����ͼ2����ͼ1�е���ADE��A����ʱ����ת��ͼ2��ʾλ�ã������������䣬��1���н����Ƿ�ı䣿��˵�����ɣ�
��3����ͼ3����ͼ1�е���ADE��A��˳ʱ����ת��ͼ3��ʾλ�ã���C��D��E���㹲�ߣ���AE=2��AC=![]() ����ֱ��д���߶�BE�ij��� ����
����ֱ��д���߶�BE�ij��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB = BC��D��E��F�ֱ���BC��AC��AB���ϵ��е㣻
��1����֤���ı���BDEF�����Σ���2����AB =12cm��������BDEF���ܳ�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У���֪![]() ��
��![]() ��
��![]() ��
��
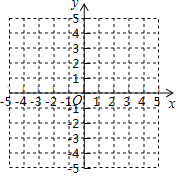
��1����ͼ�л���![]() ��
��![]() �������_____________��
�������_____________��
��2������![]() ���
���![]() ����
����![]() ��Գƣ����
��Գƣ����![]() ������Ϊ_____________��
������Ϊ_____________��
��3����֪![]() Ϊ
Ϊ![]() ����һ�㣬��
����һ�㣬��![]() �����Ϊ
�����Ϊ![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��
(1)��֤������mΪ�κ�ʵ�����˺���ͼ����x�������������㣻
(2)���˺���ͼ����x���һ������Ϊ��-3��0������˺���ͼ����x�����һ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ��ʽ��
��1���ⲻ��ʽ![]() �����ѽ⼯�������ϱ�ʾ������
�����ѽ⼯�������ϱ�ʾ������
��2���ⲻ��ʽ��![]() ��
��
��3���ⲻ��ʽ��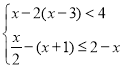 ��д�����������⣮
��д�����������⣮
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
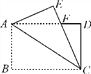
����Ŀ����ͼ������ֽƬABCD�У�AB=4��BC=6������ABC��AC�۵���ʹ��B���ڵ�E����CE��AD�ڵ�F����DF�ij�����_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ�������У�����Rt��ABC�У�AB=AC����CAB=90����A��0��a����B��b��0����

��1����ͼ1����![]() +��a-2��2=0�����ABO�������
+��a-2��2=0�����ABO�������
��2����ͼ2��AC��x�ύ��D�㣬BC��y�ύ��E�㣬����DE��AD=CD����֤����ADB=��CDE��
��3����ͼ3���ڣ�1���������£�����P��0��-6��Ϊֱ�Ƕ��㣬PCΪ��������Rt��PQC������BQ����֤��AP��BQ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCD�������Խ��߷ֱ�Ϊ6��8��M��N�ֱ��DZ�BC��CD���е㣬P�ǶԽ���BD��һ�㣬��PM+PN����Сֵ=___��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com