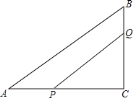
【题目】如图，
中，
，
，
，点
从
点出发向点
以
的速度移动，点
从
点出发向点以
的速度移动，当其中一点首先到达终点时运动停止，若、分别同时从，出发，几秒后四边形
是面积的
？
【答案】点
，
出发
秒后可使四边形
是
面积的
．
【解析】
由于四边形APQB是一个不规则的图形，不容易表示它的面积，观察图形，可知S四边形APQB=S△ABC﹣S△PCQ，因此当四边形APQB是△ABC面积的时，△PCQ是△ABC面积的
，即有S△PCQ=S△ABC．
△ABC中，∵∠C=90°，∴△ABC是直角三角形，由勾股定理，得：BC=
=6．
设t秒后四边形APQB是△ABC面积的，则t秒后，CQ=BC﹣BQ=6﹣t，PC=AC﹣AP=8﹣2t．
根据题意，知S△PCQ=S△ABC，∴
CQ×PC=×AC×BC，即（6﹣t）（8﹣2t）=××8×6，解得：t=2或t=8（舍去）．
答：点P，Q出发2秒后可使四边形APQB是△ABC面积的．
科目：初中数学 来源： 题型：
【题目】已知二次函数的图象与x轴交于A（﹣2，0）、B（4，0）两点，且函数经过点（3，10）．
（1）求二次函数的解析式；
（2）设这个二次函数的顶点为P，求△ABP的面积；
（3）当x为何值时，y≤0．（请直接写出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的布袋里装有4个标有1，2，3，4的小球，它们的形状、大小完全相同，小明从布袋里随机取出一个小球，记下数字为
，小红在剩下的3个小球中随机取出一个小球，记下数字为
。
(1)计算由、确定的点
在函数
的图象上的概率；
(2)小明和小红约定做一个游戏，其规则为：若、满足
＞6则小明胜，若、满足＜6则小红胜，这个游戏公平吗？说明理由.若不公平，请写出公平的游戏规则.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，A（﹣
，0）、B（0，1）分别为x轴、y轴上的点，△ABC为等边三角形，点P（3，a）在第一象限内，且满足2S△ABP=S△ABC，则a的值为（ ）
A.
B.
C.D.2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），P为△ABC所在平面上一点，且∠APB=∠BPC=∠CPA=120°，则点P叫做△ABC的费马点．
（1）如果点P为锐角△ABC的费马点，且∠ABC=60°．
①求证：△ABP∽△BCP；
②若PA=3，PC=4，则PB= ．
（2）已知锐角△ABC，分别以AB、AC为边向外作正△ABE和正△ACD，CE和BD 相交于P点．如图（2）
①求∠CPD的度数；
②求证：P点为△ABC的费马点．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=ax2+bx+c（a≠0）中自变量x和函数值y的部分对应值如下表：
x | … | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| … |
y | … | ﹣ | ﹣2 | ﹣ | ﹣2 | ﹣ | 0 |
| … |
从上表可知，下列说法正确的个数是（ ）
①抛物线与x轴的一个交点为（﹣2，0）；
②抛物线与y轴的交点为（0，﹣2）；
③抛物线的对称轴是：x=1；
④在对称轴左侧，y随x增大而增大．
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出以下结论：①abc＜0 ②b2﹣4ac＞0 ③4b+c＜0 ④若B（﹣
，y1）、C（﹣
，y2）为函数图象上的两点，则y1＞y2⑤当﹣3≤x≤1时，y≥0，
其中正确的结论是（填写代表正确结论的序号）__________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
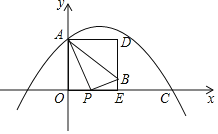
【题目】抛物线
过点
和
，点P为x轴正半轴上的一个动点，连接AP，在AP右侧作
，且
，点B经过矩形AOED的边DE所在的直线，设点P横坐标为t．
求抛物线解析式；
当点D落在抛物线上时，求点P的坐标；
若以A、B、D为顶点的三角形与
相似，请直接写出此时t的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
