
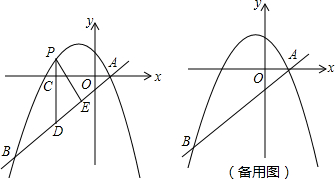
分析 (1)先由交点式得到抛物线与x轴的交点坐标为(2,0)、(-4,0),即A(2,0),再将A点坐标代入y=$\frac{3}{4}$x+b可解得b=-$\frac{3}{2}$,则直线AB的解析式为y=$\frac{3}{4}$x-$\frac{3}{2}$,接着利用一次函数图象上点的坐标特征确定B(-6,-6),然后将B坐标代入抛物线解析式求出a即可;
(2)①直线AB与y轴的交点为M,如图1,则M(0,-$\frac{3}{2}$),AM=$\frac{5}{2}$,设P(x,-$\frac{3}{8}$x2-$\frac{3}{4}$x+3),则PD=-$\frac{3}{8}$x2-$\frac{3}{2}$x+$\frac{9}{2}$,C(x,0),先证明△AOM∽△ACD得到AD=$\frac{5}{4}$(2-x),再证明Rt△ACD∽Rt△PED,根据相似三角形的性质,当△PDE的周长与△ADC的周长相等时,Rt△ACD≌Rt△PED,所以AD=PD,即-$\frac{3}{8}$x2-$\frac{3}{2}$x+$\frac{9}{2}$=$\frac{5}{4}$(2-x),解得x1=-$\frac{8}{3}$;x2=2(舍去),于是得到C点横坐标为-$\frac{8}{3}$,然后利用△PDE周长=△PCD的周长=AC+CD+AD=2-x-$\frac{3}{4}$x+$\frac{3}{2}$+$\frac{5}{4}$(2-x)=6-3x进行计算;
②分类讨论:当点P在x轴上方,如图2,作PH⊥x轴于H,设P(x,-$\frac{3}{8}$x2-$\frac{3}{4}$x+3),易得Rt△PAH∽Rt△AQO,则$\frac{PH}{OA}$=$\frac{PA}{AQ}$,当PA:AQ=4:1时,PH=4OA=8(不合题意舍去),当PA:AQ=1:4时,PH=$\frac{1}{4}$OA=$\frac{1}{2}$,即y=$\frac{1}{2}$,即-$\frac{3}{8}$x2-$\frac{3}{4}$x+3=$\frac{1}{2}$,即得x1=$\frac{-3+\sqrt{69}}{3}$,x2=$\frac{-3-\sqrt{69}}{3}$;当点P在x轴下方时,如图3,用同样方法可求得P($\frac{-3-\sqrt{93}}{3}$,-$\frac{1}{2}$),于是得到满足条件的P点坐标为($\frac{-3+\sqrt{69}}{3}$,$\frac{1}{2}$)或($\frac{-3-\sqrt{69}}{3}$,$\frac{1}{2}$)或($\frac{-3-\sqrt{93}}{3}$,-$\frac{1}{2}$).
解答 解:(1)∵抛物线解析式为y=a(x-2)(x+4),
∴抛物线与x轴的交点坐标为(2,0)、(-4,0),即A(2,0),
将A(2,0)坐标代入y=$\frac{3}{4}$x+b,解得b=-$\frac{3}{2}$,
∴直线AB的解析式为y=$\frac{3}{4}$x-$\frac{3}{2}$,
当x=-6代入y=$\frac{3}{4}$x-$\frac{3}{2}$=-6,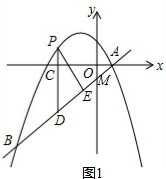
∴B(-6,-6)
将B(-6,-6)代入抛物线解析式得-6=a(-6-2)(-6+4),解得:a=-$\frac{3}{8}$,
∴y=-$\frac{3}{8}$(x-2)(x+4)=-$\frac{3}{8}$x2-$\frac{3}{4}$x+3;
故答案为2,-$\frac{3}{2}$,-$\frac{3}{8}$;
(2)①直线AB与y轴的交点为M,如图1,M(0,-$\frac{3}{2}$),AM=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$,、
设P(x,-$\frac{3}{8}$x2-$\frac{3}{4}$x+3),则PD=-$\frac{3}{8}$x2-$\frac{3}{4}$x+3-$\frac{3}{4}$x+$\frac{3}{2}$=-$\frac{3}{8}$x2-$\frac{3}{2}$x+$\frac{9}{2}$,C(x,0),
∵OM∥PD,
∴△AOM∽△ACD,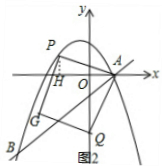
∴$\frac{AM}{AD}$=$\frac{AO}{AC}$,即$\frac{\frac{5}{2}}{AD}$=$\frac{2}{2-x}$,AD=$\frac{5}{4}$(2-x)
∵∠PDE=∠ADC,
∴Rt△ACD∽Rt△PED,
∵△PDE的周长与△ADC的周长相等,
∴Rt△ACD≌Rt△PED,
∴AD=PD,即-$\frac{3}{8}$x2-$\frac{3}{2}$x+$\frac{9}{2}$=$\frac{5}{4}$(2-x),
整理得3x2+2x-16=0
解得:x1=-$\frac{8}{3}$;x2=2(舍去),
∴C点横坐标为-$\frac{8}{3}$,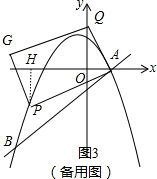
△PDE周长=△PCD的周长=AC+CD+AD=2-x-$\frac{3}{4}$x+$\frac{3}{2}$+$\frac{5}{4}$(2-x)=6-3x=6-3×(-$\frac{8}{3}$)=14;
②当点P在x轴上方,如图2,作PH⊥x轴于H,设P(x,-$\frac{3}{8}$x2-$\frac{3}{4}$x+3),
∵四边形APGQ为矩形,
∴∠PAQ=90°,
∴∠PAH=∠AQO,
∴Rt△PAH∽Rt△AQO,
∴$\frac{PH}{OA}$=$\frac{PA}{AQ}$,
当PA:AQ=4:1时,PH=4OA=8(不合题意舍去),
当PA:AQ=1:4时,PH=$\frac{1}{4}$OA=$\frac{1}{2}$,即y=$\frac{1}{2}$,
∴-$\frac{3}{8}$x2-$\frac{3}{4}$x+3=$\frac{1}{2}$,即得x1=$\frac{-3+\sqrt{69}}{3}$,x2=$\frac{-3-\sqrt{69}}{3}$,此时P点坐标为($\frac{-3+\sqrt{69}}{3}$,$\frac{1}{2}$)或($\frac{-3-\sqrt{69}}{3}$,$\frac{1}{2}$);
当点P在x轴下方时,如图3,用同样方法可求得P($\frac{-3-\sqrt{93}}{3}$,-$\frac{1}{2}$),
综上所述,满足条件的P点坐标为($\frac{-3+\sqrt{69}}{3}$,$\frac{1}{2}$)或($\frac{-3-\sqrt{69}}{3}$,$\frac{1}{2}$)或($\frac{-3-\sqrt{93}}{3}$,-$\frac{1}{2}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和一次函数图象上点的坐标特征;会利用待定系数法求函数解析式;理解坐标与图形性质;灵活运用相似三角形的判定与性质解决几何计算;会解一元二次方程.


科目:初中数学 来源: 题型:选择题
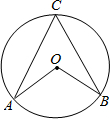 如图,∠ACB和∠AOB是⊙0中弧AB所对的圆周角和圆心角,∠AOB=80°,则弧AB所对圆周角的度数是( )
如图,∠ACB和∠AOB是⊙0中弧AB所对的圆周角和圆心角,∠AOB=80°,则弧AB所对圆周角的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{{h}_{1}}{{h}_{2}}}$ | B. | $\frac{\sqrt{{h}_{1}}}{\sqrt{{h}_{2}}}$ | C. | $\frac{\sqrt{{h}_{1}{h}_{2}}}{{h}_{2}}$ | D. | $\frac{\sqrt{{h}_{1}{h}_{2}}}{{h}_{1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某超市一批灯泡的使用寿命 | |
| B. | 调查电视节目《中国好声音》的收视率 | |
| C. | 了解全国中学生视力情况 | |
| D. | 了解乘坐飞机的旅客是否携带了危险品 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{a^2}-2a+2}$ | B. | $\sqrt{3b}$ | C. | $\sqrt{x+1}$ | D. | $\sqrt{1-{y^2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com